Vektoren: Vom Fußpunkt des Leuchtturmes sieht man die beiden Schiffe A und B unter einem Winkel von 166°...

Question

vom Fußpunkt eines an der Meeresküste stehenden Leuchtturmes mit der Höhe h = 37,5 m sieht man die beiden Schiffe A und B unter einem Winkel von 166°. Vom Schiff A aus sieht man die Spitze des Turmes unter dem Höhenwinkel von 27,6°, vom Schiff B aus unter dem Höhenwinkel von 36,5°. Wie weit sind die beiden Schiffe voneinander entfernt? Beachte, dass der Fußpunkt des Turms und die beiden Schiffe in derselben Horizontalebene liegen.

Answer 1

Schiff, Fußpunkt, Turmspitze bilden ein rechtwinkeliges Dreieck. Aus Turmhöhe und Höhenwinkel kannst du also mittels Tangens die Entfernung des Schiffes vom Leuchtturm berechnen.

Wenn du das für beide Schiffe gemacht hast kannst du mit dem Kosinussatz \( c²=a²+b²-2ab\cos\gamma \) die Entfernung der Schiffe untereinander berechnen.

Answer 2

Am besten betrachtest du erst mal das Dreieck von Schiff A zu Leutturmboden X und Leutturmspitze S

Da der Leutturm senkrecht steht ist das rechtwinklig:

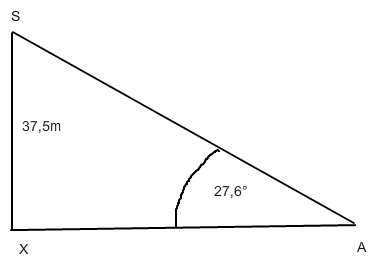
Damit gilt  tan( 27,6°) = 37,5m / XA   also   XA = 37,5m / tan(27,6°) = 71,7 m

Entsprechend für das Schiff B gibt  XB = 37,5m / tan( 36,5° ) = 50,7 m

Dann hast du in dem Dreieck XAB jetzt zwei Seiten von 50,7m und 71,7m

und zwischen diesen (bei X ) einen Winkel von 166° . So bekommst du die

gesuchte Länge von A nach B mit dem cos-Satz.

Answer 3

d = h·√(COT(α)^2 + COT(β)^2 - 2·COT(α)·COT(β)·COS(γ))

d = 37.5·√(COT(27.6°)^2 + COT(36.5°)^2 - 2·COT(27.6°)·COT(36.5°)·COS(166°)) = 121.5 m

Hast du dir bereits eine Skizze angefertigt ?

Comments

Eine Skizze könnte wie folgt aussehen: