Bei Aufgabe 1) lässt sich für die Berechnung von a der Kosinussatz anwenden:
a2 = b2 + c2 - 2bc * cos(α) | √
a = √(b2 + c2 - 2bc * cos(α))
Wenn man nun die gegebenen Werte einsetzt, ergibt sich:
a = √(122 + 92 - 2 * 12 * 9 * cos(64°))
a = √(225 - 216 * cos(64°))
a ≈ 11,415
Die anderen beiden Winkel lassen sich nun ggf. noch mit dem Sinussatz bestimmen.
Für den Flächeninhalt benötigt man die Höhe von einer Seite. Die Formeln dafür lauten:
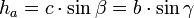
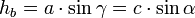
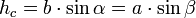
Da wir jetzt den Winkel α schon gegeben haben, ist es günstig, entweder hb oder hc zu berechnen. Ich entscheide mich mal für hb.
hb = c * sin(α)
hb = 9 * sin(64°)
hb ≈ 8,089
Der Flächeninhalt A ist dann:
A = 1/2 * b * hb
A = 1/2 * 12 * 9 * sin(64°)
A = 54 * sin(64°)
A ≈ 48,535
Dann noch zu Aufgabe 2). Funktioniert im Prinzip genauso, nur dass es hier praktischer ist, zunächst die anderen Winkel auszurechnen und dann die fehlende Seitenlänge. Dazu verwendet man zunächst für γ den Sinussatz:
a / sin(α) = c / sin(γ) | * sin(α) | * sin(γ)
a * sin(γ) = c * sin(α) | / a
sin(γ) = c * sin(α) / a | sin-1
γ = sin-1(c * sin(α) / a)
Dann die Werte einsetzen und ausrechnen:
γ = sin-1(11,3 * sin(108°) / 15,4)
γ ≈ 44,255°
Da die Summe aller Winkel eines Dreiecks immer 180° beträgt, können wir β ganz schnell ausrechnen:
β = 180° - α - γ
β ≈ 180° - 108° - 44,255°
β ≈ 27,745°
Und nun können wir die Seitenlänge b, jetzt wo wir β haben, ebenfalls mit den Sinussatz berechnen:
b / sin(β) = a / sin(α) | * sin(β)
b = sin(β) * a / sin(α)
b ≈ sin(27,745°) * 15,4 / sin(108°)
b ≈ 7,538
So, und an den Flächeninhalt kannst du dich ja jetzt mal selbst versuchen. Funktioniert genauso wie in Aufgabe 1). ^^