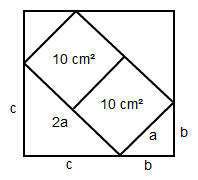
Die Seitenlänge a des kleinen Quadrats mit 10 cm² lässt sich berechnen durch:
a = √10
Dies ist dann die Hypotenuse des Dreiecks unten rechts. Die Katheten haben jeweils die Seitenlänge b. Also gilt nach Pythagoras:
b² + b² = a²
2b² = a² | ÷ 2
b² = a²/2 | √
b = √(a²/2)
Wenn wir nun das für a den zuvor berechneten Wert √10 einsetzen, ergibt sich also:
b = √((√10)²/2)
b = √(10/2)
b = √5
So, dann brauchen wir jetzt nur noch c auszurechnen. Dies funktioniert in dem großen Dreieck unten links genauso, nur dass die Hypotenuse diesmal 2a ist.
c² + c² = (2a)²
2c² = 4a² | ÷ 2
c² = 2a² | √
c = √(2a²)
c = √(2(√10)²)
c = √(2 * 10)
c = √20
Die gesamte Seitenlänge des Dreiecks ABCD beträgt also:
b + c = √5 + √20
b + c ≈ 6,708