Kreisausschnitte berechnen mit Hilfe von Satz des Pythagoras

Question

Hallo könnt ihr mir diese aufgabe in einfachen Schritten erklären:

Gesucht wird die Größe der gefärbten Fläche für r = 4 cm

Ohne Pythagoras geht es nicht!

Answer 1

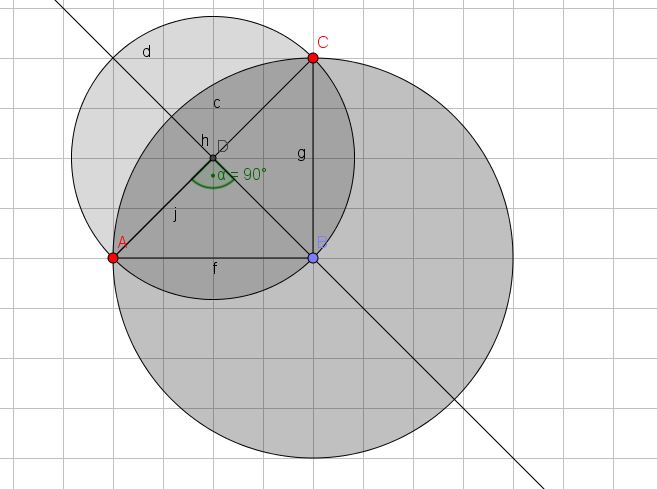
Wie du hoffentlich anhand der Zeichnung erkennst, brauchst du den Pythagoras, um den Radius des kleinen Kreises berechnen zu können. Der Durcmesser dieses Kreises ist die Hypotenuse des Dreiecks ABC. Mit dem Pythagoras - den Rechenweg spare ich mir jetzt - ergibt sich eine Länge von 5,66 cm. Der Radius beträgt also 2,83 cm. Der zu berechnende Kreisausschnitt ist der "kleine" Halbkreis minus der Fläche, die von der Strecke AC und dem Kreisbogen des größeren Kreises begrenzt wird. Diesen Teil kann man berechnen, indem man den Flächeninhalt des Dreiecks ABC von dem Flächeninhalt des Viertelkreises des größeren Kreises subtrahiert. Also:

Fläche des kleinen Halbkreises: π*2,83²/2 = 12,58 cm²

Fläche des Viertes des größeren Kreises: π*4²/4 = 12,57

Flächeninhalt des Dreiecks: 5,66*2,83/2= 8,01 Diese Zahl von 12,57 abgezogen ergibt 4,56. Diese Zahl von den 12,58 subrahiert ergibt 8,02 cm² Flächeninhalt