Lösung meiner Ungleichung richtig?

Question

Hi.

Da ich gestern Hilfe vom Board hier bekam wie ich etwas zu rechnen habe, würde ich jetzt gerne wissen, ob ich dies auch richtig getan habe.

Aufgaben waren: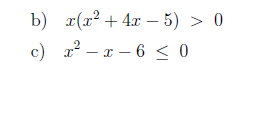

So erstmal Aufgabe c)

Habe die PQ Formel gemacht dadurch kam dann halt x1/2 = - (-1/2) +- √(-1/2)² -(-6)

So da bekam ich dann 3 und -2 raus und Die Lösungsmenge ist dann:

L = [-2,3] = x Elemente R | -2 < x < 3 )

Ist das so richtig? Was mich etwas stutzig macht ist, dass wenn ich in meine Untelragen schaue, wir immer sowas haben wie "Fall 1" und "Fall 2" etc.

Beispielsweise hatten wir die Aufgabe (24 +x)/x  + 1 < 4. Da haben wir 1.Fall gehabt mit x>0 und dann später Fall 2 mit x < 0. Ist das notwendig bzw. muss ich das bei meiner Aufgabe auch tun? Weil ich das nicht wirklich verstanden hatte.

So zu c:  x(x² + 4x - 5) > 0

Erste x ist bereits 0 und dann habe ich (x² +4x -5) > 0 mithilfe des Satzes von Vieta gemacht und bekam dann:

-1 * 5 = q

-(-1 +5) = p

also x1 = 0   x2 = -1    x3 = 5

Ist das so richtig? Auch hier wieder meine Frage mit 1. Fall und 2. Fall etc :/ In der Vorlesung war nicht wirklich die Zeit für mich da das nachzuvollziehen wann man so etwas macht und wann eben nicht. :/ 

Answer 1

So zu c:  x(x² + 4x - 5) > 0

Erste x ist bereits 0  Falsch

Du sollst nicht lösen
x(x² + 4x - 5) = 0
sondern
x(x² + 4x - 5) > 0

Fall 1
plus *  plus
( x > 0 ) und ( x^2 + 4x - 5  > 0 )

Fall 2
minus * minus
( x < 0 ) und ( x^2 + 4x - 5  < 0 )

Und jetzt beides berechnen.

Deine Lösung für
x^2 + 4x - 5  = 0
ist auch falsch
x^2 + 4x - 5 = ( x + 5 ) * ( x - 1 )
x = -5 und x = 1

Comments

Und was meinst du mit plus * plus und minus * minus? 

Das lass ich ja dann so x > 0, wenn ich das richtrig verstanden habe und bei x² + 4x - 5  > 0  muss ich doch aber PQ Formel machen oder nicht? 

Nur versteh ich nicht, was du mit Fall 1 plus * plus meinst und Fall 2 minus * minus.

Und zu 2 hm okay, dann habe ich mich da wohl vertan. hatte den Satz von Vieta zum ersten mal angewendet und zufälligerweise hat da ein YouTuber die gleichen zahlen gehabt aber bekam dann 5 und -1 raus. 

Der hatte nämlich gesagt, dass -1 * 5 = -5 ergeben würde, was ja dann q wäre

---

Die Ungleichung

x(x² + 4x - 5) > 0

wird dann wahr wenn

der erste Faktor > 0 ist
und
der 2.Faktor größer 0 ist denn
plus mal plus ergibt plus

oder
der erste Faktor < 0 ist
und
der 2.Faktor kleiner 0 ist denn
minus mal minus = plus

Ich rechne dir den 1.Fall einmal zuende.

---

Oh das wäre sehr nett, wenn du mir das mal zeigst mit den erste Faktor < 0 etc, weil ich das echt 0 verstehe 

---

Hier die Berechnungen






mfg Georg

---

Oh mein gott wie nett von dir wie kann ich das wieder gut machen. Ist ja heftig. Danke für deine Mühe.

Kannst du mir noch sagen ob denn wenigstens meine Lösung für c) richtig war? Also für x1/2 = - (-1/2) +- √(-1/2)² -(-6)

---

So

(-2) * (-2 ) = Vorzeichen der Lösung ?
(-2) * (+2 ) =
(+2) * (-2 ) =
(+2) * (+2 ) =

Antwort
(-2) * (-2 ) > 0
(-2) * (+2 ) < 0
(+2) * (-2 ) < 0
(+2) * (+2 ) > 0

---

Ich muss mich da echt noch mal ganz langsam alles genau angucken um das zu verstehen was du da alles gemacht hast ^^ 

---

Bin jetzt einkaufen. Später.

---

danke für deine Hilfe ist schon sehr enorm, was du mir da hingezaubert hast. Aber ich verstehe ehrlich gesagt den ersten Schritt nicht, wie du von

x² + 4x - 5 > 0 auf das kommst

x² + 4x +2²-2² > 5

Also alles erschließt sich mir aber nicht wie du auf die +2²-2² kommst

---

Kleine Anmerkung: Du benutzt das "und" mal wie das logische "und" und mal aufzählend (richtig wäre an diesen Stellen "oder"). 

---

Ich erlaube mir mal für Georg einzuspringen :).

Er wollte eine binomische Formel kreiieren. Dazu hatte er x^2+4x zur Verfügung. Da hat er erkannt er muss 2^2 hinsetzen. Da man aber nicht einfach eine Zahl addieren darf, muss er sie gleich wieder abziehen.

Das führt zu 2^2 - 2^2. Und das ist in der Tat 0. Er hat also nichts geändert, hat aber doch was er will/braucht :).

Grüße

---

Ahhhhhhhhhhhhhhhhhhhh jetzt verstehe ich. Ja das mit der binomische formel hatte ich sogar erkannt aber ich wusste nicht, dass man dann einfach die hinzufügen kann und direkt wieder abziehen kann. jetzt hat es klick gemacht sehr schick danke ihr seid wirklich eine große hilfe :) 

---

Kein Ding :).

---

Weiß denn jemand ob meine andere Aufgabe richtig ist mit der PQ Formel da und der Lösungsmenge? 

Also das hier:

Habe die PQ Formel gemacht dadurch kam dann halt x1/2 = - (-1/2) +- √(-1/2)² -(-6)

So da bekam ich dann 3 und -2 raus und Die Lösungsmenge ist dann:

L = [-2,3] = x Elemente R | -2 < x < 3 )

---

Ja, das ist richtig!          

---

Yeah sehr gut dann bin ich jetzt happy. Dann :) 

---

@jc2055
Zur Information :
Deine Kommentare bezüglich " und " und " oder "
sind  zwecklos.
Ich werde mich nicht mehr ändern.
Ich bin 62. Bei mir hat der Altersstarrsinn schon
lange begonnen.

@shaKi47
Ich habe den Eindruck die Mathematik in diesen Strang
liegt bei dir wie " Kraut und Rüben " vor.

Die gute Nachricht : das läßt sich ändern.
Du nimmst an einem Matheunterricht teil,
im Internet oder hier beim Forumsbetreiber gibt
es Videos oder Nachhilfe
und zuletzt muß gerechnet und geübt werden.

Durch die Bewältung von Problemen lernt am
meisten.
Deshalb auch : hier immer schön Fragen stellen.

Die Antwortgeber werden es dir danken das sie
etwas zu tun bekommen.

---

Schade, dass du nichts mehr lernen möchtest ist deine Sache. Anderen aber einen falschen Stil zu zeigen ist fahrlässig. Das war mein erster Kommentar aber aus deiner Reaktion geht hervor, dass dies nicht der erste und auch nicht der letzte Hinweis an dich in diese Richtung sein wird.

---

@georgborn

Na ich nehme ja schon extra an den freiwilligen Tutorien meiner Universität teil, wo jemand im 10 Semester Mathematik studiert und es unterrichtet. Aber leider wurde aus zeitlichen Gründen, der Abschnitt mit den "Fällen" überhaupt nicht beleuchtet. Bzw. wir machen zurzeit Mengenoperationen. Das habe ich wunderbar noch verstanden, weil es am Anfang des Unterrichts stattfand. Aber für das mit den Fällen bleib überhaupt keine Zeit für Erklärungen...

Dann habe ich mir ein Video vorhin angeschaut zur Erläuterung des Satzes von Vieta und der hatte exakt die selben Zahlen wie ich und kam dann auf das Ergebnis was ich am Anfang geschrieben hatte. Deswegen war ich auch komplett verwirrt, wieso das Vorzeichen bei dir anders war. Aber ich bemühe mich schon immer, dass alles zu verstehen. Meistens verstehe ich es auch beispielsweise deins habe ich jetzt verstanden, aber wenn dann andere Zahlen kommen und ein paar Tage dazwischen liegen, ist das fast immer schon wieder weg. :-/ 

---

@ij2088
Schade, dass du nichts mehr lernen möchtest ist
Dies scheint auch für dich zu gelten.
Obwohl ich angab : deine Kommentare bezüglich " und " und
" oder "  sind  zwecklos. willst du es weiter versuchen ?
Eine eigene korrekte Antwort einzustellen steht in deinem
Belieben.
Von Beileidsbezeugungen an meinem Grab bitte ich zudem
Abstand zu nehmen.

---

Kannst du mir eigentlich noch einige Fragen dazu beantworten?

1. Wo ist das x vor der Klammer hin?

2. Bei der b) kommst du aufeinmal auf -3. Wieso ist bei a) noch 3 und bei b) aufeinmal -3? 

---

ich nehme an du meinst das Handschriftliche

x * ( x² + 4x - 5) > 0

1.Blatt
gilt für x > 0
Der erste Faktor des Produkts ist größer 0.

Es gibt, wie bei relativ vielen quadratischen Gleichungen
2 Lösungen

Der Term
( x² + 4x - 5) > 0
wurde umgeformt zu
( x + 2 )^2 > 9
Der linke Teil ist ein Quadrat.
Falls der Wert in der Klammer > 3 ist
oder
< -5  ist ( x = -6 ; ( -6 + 2 ) = -4 zum Quadrat = 16
ist gehört er zur Lösung.

Ich muß feststellen : an deinem elementaren  Grundwissen
muß noch etwas getan werden. Ist nicht bös gemeint.
Dies ist ein Fakt.

---

Ja ich tue mein bestes ^^ Ich habs aber zu meiner Verteidigung auch einen Freund gezeigt der im Leistungskurs ist und sogar eine 1 hat und der wusste es auch nicht ^^ 

---

Die Aufgaben könnten aus der 11. oder 12.Klasse sein und sind
nicht sonderlich schwierig.

Falls du dich verbesseren willst. es gibt nur einen auf dieser Welt
der dich am Schopf packen kann und aus dem Sumpf zieht.
Und das bist du selbst.