Wie führe ich eine Sensitivitätsanalyse bei linearer Optimierung durch?

Question

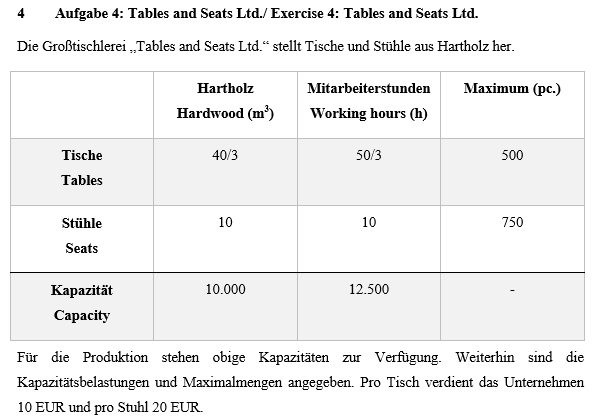
In der Aufgabe habe ich bereits Folgendes ermittelt: Optimierungsproblem: Max f(x₁,x₂) : = 10x₁ + 20x₂ = Z

1. NB: x₁ + 10x₂ ≤ 10.000    2. NB: x₁ + 10x₂ ≤ 12.500   3. NB: x₁ ≤ 500      4. NB: x₂ ≤ 750

x₁ : Anzahl Tische       x₂ : Anzahl der Stühle y_1-4 : Hilfsvariablen zu den Nebenbedingungen 1.-4.

Durch den Simplex-Algorithmus habe ich ein Endtableau erhalten, das aussagt:

x₁ = 187,5        x₂ = 750           y₁ = 0               y₂ = 1.875        y₃ = 312,5        y₄= 0               Z= 16.875

Bei allen drei Teilaufgaben soll ich eine Sensitivitätsanalyse durchführen, nur leider weiß ich nicht genau wie man diese mathematisch erstellt. Kann mir vielleicht jemand einen Tipp geben?

1.) Wieviel Mitarbeiterkapazität kann das Unternehmen abbauen, ohne dass sich das optimale Ergebnis ändert?

2.) Auf welchen Preis kann der Preis für Tische erhöht werden, ohne dass sich das optimale Ergebnis ändert?

3.) Um wieviel kann die Maximalmenge für Tische gesenkt werden, ohne dass sich das optimale Ergebnis ändert?

Comments

Durch y₂ der 2.NB kann ich ja schon ablesen, dass 1.875 Stunden bei der Mitarbeiterkapazität "über" sind, aber das ist ja keine vollständige Sensitivitätsanalyse, oder?

Answer 1

Vielleicht könnte man Vergleichswerte oberhalb und unterhalb der 1.875 einsetzen und damit zeigen, dass es nur das schon bereits errechnete Ergebnis sein kann?