Ellipse in 1. Hauptlage mit Tangente t: 4x+9y=75, und Berührungspunkt P(p1/3)

Question

Von einer Ellipse in 1. Hauptlage sind eine Gleichung der Tangente t sowie de Berühungspunkt P gegeben. Ermittle eine Gleichung der Ellipse!

a) t: 4x+9y=75, P(p₁/3)

bitte mit Rechenschritte

danke

Comments

Bei einer Ellipse in 1. Hauptlage liegen die Brennpunkte, wenn ich das richtig im Kopf habe, auf der x-Achse. Zudem ist die y-Achse symmetrisch.

B1(-a|0) und B2(a|0)

Für Punkte P(x|y) auf der Ellipse gilt: (x+e)^2 + y^2 + (x-e)^2 + y^2 = konstant.

Prüfe das mit der 1. Hauptlage zuerst, wenn du die Ellipsengleichung herleitest.

Ellipsengleichung (a>b)

b^2 x^2 + a^2 y^2 = a^2 b^2

oder

x^2/a^2 + y^2/b^2 = 1

Du brauchst y=… damit du ableiten kannst.

a^2 y^2 = a^2 b^2 - b^2 x^2

y^2  = b^2 - (b/a)^2 x^2

y = ±√ (b^2 - (b/a)^2 x^2)

y= ±b√(1 - a^2/x^2)

---

zeigen sie es mir bitte vor weil das haben wir nicht in der schule gemacht vielen Dank

---

Das mit der 1. Hauptlage scheint zu stimmen. Ich passe oben mal noch die Bezeichnungen an. Vgl. S. 7 in folgendem Skript:

http://www.mathe-online.at/materialien/stefanie.mandl/files/NeuesVerzeichnis/Kegelschnitte/Ellipse.pdf

Answer 1

a) t: 4x+9y=75, P(p₁/3)

Weil P auf t liegt, gilt

4p₁ + 27 = 75

4p₁ = 48

p₁ = 12

P einsetzen in:

b² x² + a² y² = a² b²

I. 144 b^2  + 9a^2 = a^2 b^2.

Steigung der Tangente. 9y = 75 - 4x

y = 75/9 - 4/9 x

m = -4/9

y=  b√(1 - a²/x²) nach x ableiten. (Beachte: - kann man weglassen, da P oberhalb der x-Achse liegt.)

x=12 in Ableitung einsetzen und gleich -4/9 setzen.

y= b√(1 - a²x^-2)

y' = b*(0.5 / √(1 - a²/x²)  )* (-2)(-a^2)x^{-1}

y' = b*(0.5 / √(1 - a²/x²)  )* (2)(a^2)x^{-1}

y' = b*(1 / √(1 - a²/x²)  )* (a^2)x^{-1}

y' = a^2 b /(x √(1 - a²/x²) )

-4/9 = a^2 b / (12 √(1 - a^2/144))

II.   -4/9 = a^2 b / ( √(144 - a^2))

Nun hast du eine 2. Gleichung mit den Unbekannten a und b. Zusammen mit der Gleichung I. solltest du dann a und b rausbekommen. Ich nehme an, dass das klappt. Es ist vielleicht schlau, erst mal nachzurechnen ;-)

 

Answer 2

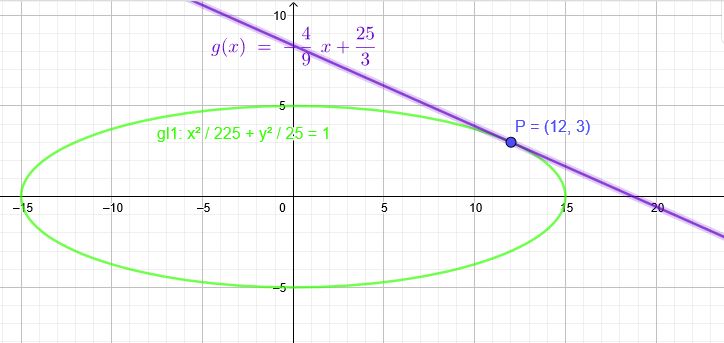
Ellipse:

\( \frac{x^2}{a^2} +\frac{y^2}{b^2}=1\)         \(y=\red{-\frac{4}{9}}x+\frac{25}{3}\),  \(P(\blue{12}|\orange{3})\):

\( \frac{144}{a^2} +\frac{9}{b^2}=1\)        \(  9a^2=b^2\cdot (a^2-144)\)      \(  b^2=\frac{9a^2}{a^2-144}\)

\( \frac{x^2}{a^2} +\frac{y^2}{\frac{9a^2}{a^2-144}}=1\)   

\( \frac{x^2}{a^2} +\frac{y^2(a^2-144)}{9a^2}=1\) 

Implizites Differenzieren:

\(f'(x)=-\frac{f_x(x,y)}{f_y(x,y)} \)

\(f_x(x,y)=\frac{2x}{a^2}\)        \(f_y(x,y)=\frac{2y(a^2-144)}{9a^2}\)

\(f'(x)=-\frac{\frac{2x}{a^2}}{\frac{2y(a^2-144)}{9a^2}} \)

\(\red{-\frac{4}{9}}=-\frac{\frac{2\cdot \blue{12}}{a^2}}{\frac{2\cdot \orange{3}(a^2-144)}{9a^2}}= -\frac{\frac{4}{a^2}}{\frac{(a^2-144)}{9a^2}}=-\frac{36}{a^2-144}\)

\(\red{\frac{1}{9}}=\frac{9}{a^2-144}\)

\(a^2=225\)      \(  b^2=\frac{9\cdot 225}{225-144}=25\)

\( \frac{x^2}{225} +\frac{y^2}{25}=1\)