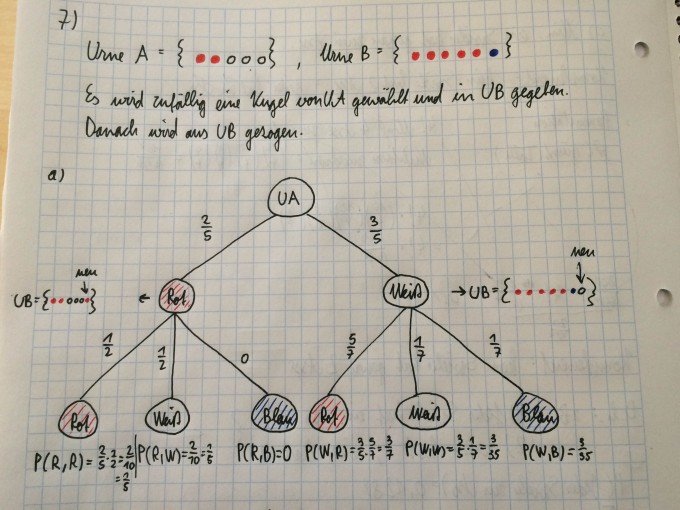
Es wird zufällig eine Kugel von Urne A gewählt und in Urne B gegeben. Danach wird aus Urne B gezogen.
a) Zeichnen Sie den W! Baum.
b) Was ist die Wahrscheinlichkeit, dass beide gezogene Kugeln rot sind?
c) Was ist die Wahrscheinlichkeit, dass die aus Urne B gezogene Kugel rot ist?
d) Nehmen wir an, die Kugel aus Urne B war rot. Wie groß ist die Wahrscheinlichkeit, dass die Kugel aus Urne A rot war?
Ich habe a), b) und c) schon probiert, aber ich kriege falsche Lösungen (laut unserer gegebenen Lösungen) raus.
Ein Bild von meinem Wahrscheinlichkeitsbaum ist im Anhang. Ich habe für meine Lösungen eigentlich nur aus dem Wahrscheinlichkeitsbaum abgelesen.
Zu b): Was ist die Wahrscheinlichkeit, dass beide gezogene Kugeln rot sind?
$$P(R,R) = \frac{2}{5} \cdot \frac{1}{2}=\frac{1}{5}=0.2$$
Meine Lösung: 1/5=0.2
Lösung laut Skript: 0.34
Zu c): Was ist die Wahrscheinlichkeit, dass die aus Urne B gezogene Kugel rot ist?
$$P(R,R) + P(W,R) = \frac{1}{5} + \frac{3}{7} = \frac{22}{35} = 0.629$$
Meine Lösung: 22/35=0.629
Lösung laut Skript: 0.77
Für d) brauche ich wahrscheinlich den Satz von Bayes, aber wenn es schon hier scheitert...
Was mache ich falsch?