Zeigen sie, dass (M,*) eine algebraische Struktur ist.

Question

ich weiß, dass ist eigentlich etwas ziemlich simples aber ich stehe irgendwie vollkommen auf dem Schlauch und mir will nicht einfallen selbst nachdem ich verschiedene Sachen mir dazu angeguckt hab wie man das zeigen kann...
Hier mal die Aufgabe:

Sei U eine nichtleere Menge und A ⊆ U. Dann ist die charakteristische Funktion χA : U → {0, 1} definiert durch

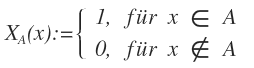
Wir bezeichnen die Menge aller charakteristischen Funktionen auf U mit

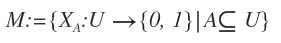
Sei die Verknupfung ∗ zwischen zwei Elementen χ_A und χ_B von M definiert durch χ_A ∗ χ_B := χ_A · χ_B, d.h.

∀ x ∈ U : (χ_A ∗ χ_B)(x) := χ_A(x) · χ_B(x).

(i)     Zeigen Sie, dass (M,*) eine algebraische Struktur ist.

(ii)    Zeigen Sie, dass (M,*) eine Halbgruppe ist.

(iii)   Zeigen Sie, dass (M,*) ein Monoid ist.

(iv)   Zeigen Sie, dass (M,*) ein kommutativ ist.

Für Halbgruppe, Monoid, und kommutativ habe ich die jeweiligen Definitionen und Beispiele aus der Vorlesung, aber irgendwie finde ich nirgends ein Beispiel wie man beweist, dass etwas eine algebraische Struktur ist... also ich weiß zwar, dass es eine ist aber ich habe gerade keine Ahnung wie ich es zeigen kann.


Philipp

Comments

Reicht es zu zeigen, dass (M,*) in sich geschlossen ist um zu zeigen, dass es eine algebraische Gruppe ist?

---

okay hat sich nun erledigt, habs jetzt gefunden ... komm mir gerade dämlich vor für die frage xD