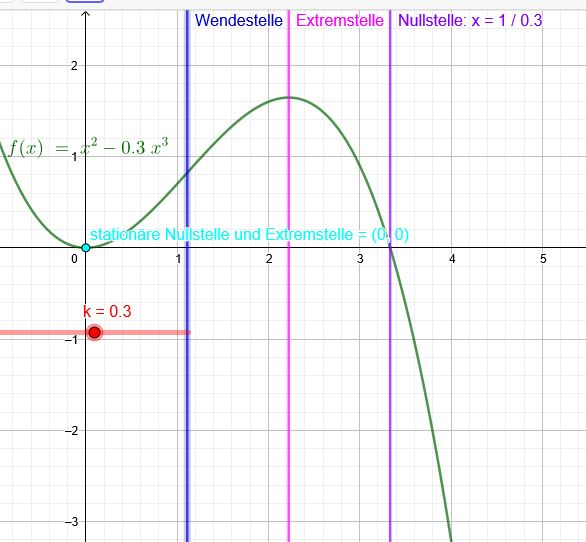
\( f_{k}(x)=x^{2}-k x^{3}, k \in \mathbb{R} \)
a) Bestimmen Sie die Nullstellen, Extremstellen und Wendestellen der Graphen der Funktionen \( \mathrm{f}_{\mathrm{k}} \).
Nullstellen:
\( x^{2}-k x^{3}=0\)
\( x^{2}(1-k x)=0\)
1.) \( x=0\) doppelte Nullstelle (stationär, da unabhängig von k)
\( 1-k x=0\)
2.) \(x_3=\frac{1}{k}\) mit \(k≠0\)
Extremstellen:
\( f'_{k}(x)=2x-3k x^{2}\)
\(2x-3k x^{2}=0\)
\(x(2-3k x)=0\)
\(x_1=0\)
\(2-3k x=0\)
\(3k x=2\)
\(x_2=\frac{2}{3k}\)
Wendestelle:
\( f''_{k}(x)=2-6k x\)
\( 2-6k x=0\)
\( x=\frac{1}{3k}\)
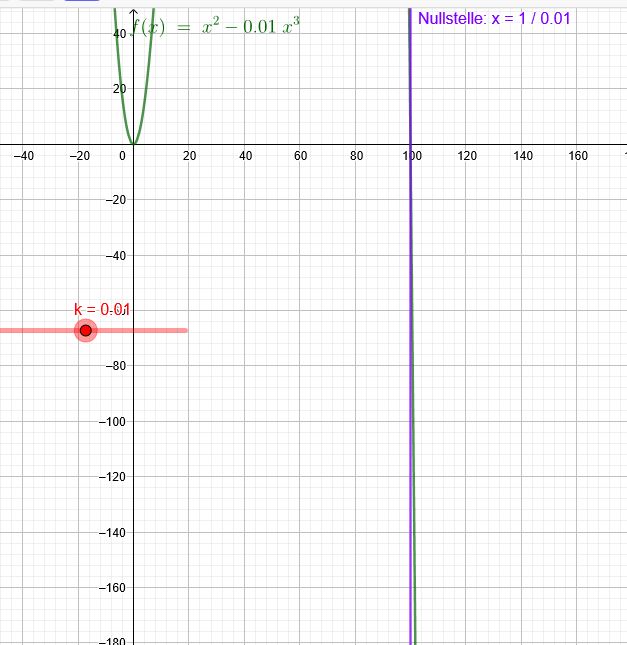
b) Für welchen Wert \( k \) hat die Funktion \( f_{k} \) an der Stelle \( x=100 \) eine Nullstelle?
\( f_{k}(100)=100^{2}-k\cdot 100^{3}=0 \)
\(100^{2}-k\cdot 100^{3}=0 \)
\(k=\frac{100^2}{100^3}=\frac{1}{100} \)
d) Welcher von allen Extrempunkten hat vom Punkt \( \mathrm{P}(0 \mid 2) \) minimalen Abstand?
Ortslinie für die beweglichen Extrempunkte:
\(x=\frac{2}{3k}\) → \(k=\frac{2}{3x}\)
\(y=x^{2}-\frac{2}{3x} x^{3}=\frac{1}{3} x^{2}\)
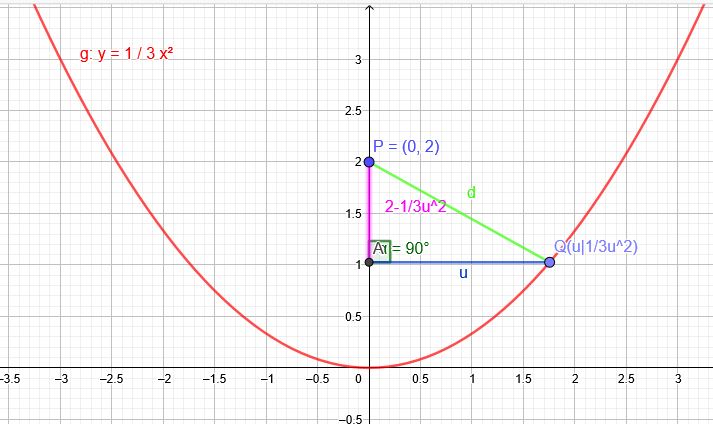
Der Abstand \(d\) der Punkte P \((0|2)\) und Q\((u| \frac{1}{3}u^2)\) soll minimal werden:
\(d^2=u^2+(2- \frac{1}{3}u^2)^2 \)
\(d(u)=\sqrt{u^2+(2- \frac{1}{3}u^2)^2} \)
\(d'(u)=\frac{2u+2(2- \frac{1}{3}u^2)\cdot(-\frac{2}{3}u)}{2\sqrt{u^2+(2- \frac{1}{3}u^2)^2}}\\= \frac{u+(2- \frac{1}{3}u^2)\cdot(-\frac{2}{3}u)}{\sqrt{u^2+(2- \frac{1}{3}u^2)^2}}=0\)
\(u_1= 0 \)
\(u_2= \sqrt{\frac{3}{2}} \)
E \((\sqrt{\frac{3}{2}} | \frac{1}{2}) \)