wo liegt der Fehler? Schnittpunkt Ellipse und gerade

Question

Hallo. Meine Aufgabe ist:

Gegeben ist Gleichung der Ellipse: 2x^2 +y^2= 2 und der Punkt p(1,0).

a) für einen (beliebigen) rationalen Parameter t bezeichne Lt die gerade durch Punkt P mit Steigung t. Stellen sie Gleichung für die gerade aus.

Meine Lösung: t= (y1-y2)/(x1-x2) Daraus folgt: t= y-0/x-1

t(x-1)=y

So in b) muss ich den Schnittpunkt von von Lt und E bestimmen.

Setze dann einfach die y in E ein:

2x^2 +(t(x-1))^2=2  jetzt bekomme ich nur 1 raus, aber den habe ich schon.

Hier bin ich stehen geblieben: 2(x^2-1) +(tx-t)^2=0

Answer 1

a) deine Gerade y = t*x - t ist ok

b) die Idee, y einzusetzen ist auch ok

2x^2+(t*x-t)^2=2

2x^2 + t^2*x^2 - 2*t^2*x + t^2=2

2x^2 + t^2*x^2 - 2*t^2*x + t^2-2=0

(2+t^2)x^2-2*t^2*x+t^2-2=0

x^2-(2t^2)/(2+t^2)*x+(t^2)/(2+t^2)-(2)/(2+t^2)=0

jetzt hast du p und q für die p-q-Formel

rechne es durch, du bekommst

x₁=(t^2+2)/(2+t^2)=1

x₂=(t^2-2)/(2+t^2)

du hast jetzt die Schnittstellen, noch in die Geradengleichung einsetzen und du hast die Schnittpunkte

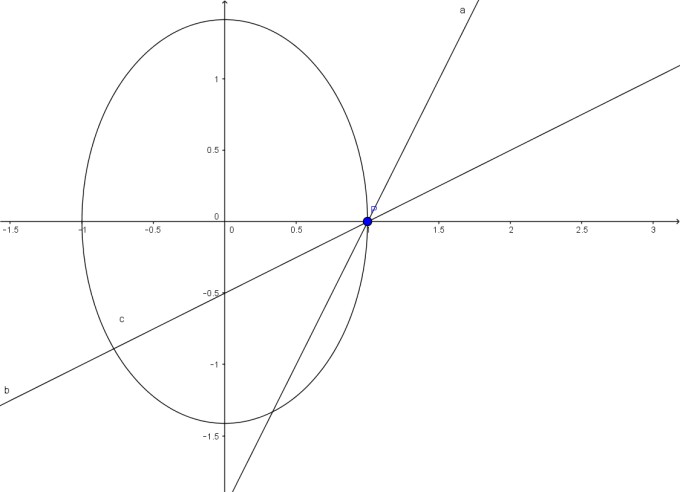
auch mal die Skizzen für t=2 (Gerade a) und t=0,5 (Gerade b)

Comments

Danke für deine Hilfe :)

---

Ich verstehe einige Schritte nicht. Wie das hier und weiter:

(2+t^2) x^2-2t^2*x +t^2-2=0

---

Um die p-q-Formel benutzen zu können, muss der Faktor vor x^2 gleich 1 sein, also ist durch 2+t^2 zu teilen

---

Ok das verstehe ich noch, aber die weiteren Schritte nicht mehr. Ich soll die ganze Gleichung durch 2+t^2 teilen. Jetzt wird es noch komplizierter

---

Ich komme nicht auf die gleiche Lösung. Kannst du mir deine Zwischenschritte zeigen?