Flächeninhalt einer Ellipse, ich finde meinen Fehler nicht.

Question

Ich habe selbst nachgerechnet und erhalte:

$$ \frac { 1 }{ 2 }\int_{0}^{2\pi}[acos(t)*acos(t)+bsin(t)*bsin(t)] dt $$
$$ \frac { 1 }{ 2 } \int_{0}^{2\pi}[a^2cos(t)^2+b^2sin(t)^2] dt $$
$$ \frac { 1 }{ 2 }\int_{0}^{2\pi}a^2*b^2 (cos(t)^2+sin(t)^2) dt $$
$$ \frac { 1 }{ 2 }\int_{0}^{2\pi}a^2*b^2 dt $$

irgendetwas habe ich falsch gemacht....

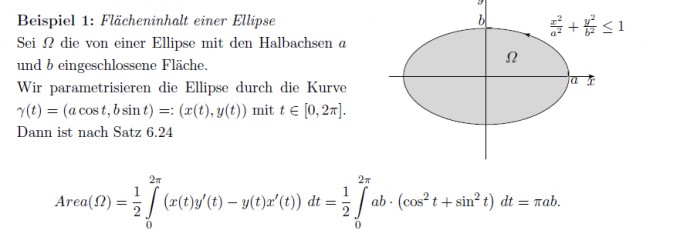
ich bin davon ausgegangen, dass x(t) = acos(t) und y(t) = bsin(t) ist.

ich würde mich freuen, wenn jemand meinen Fehler erkennt...

Dankee!

Comments

Du hast im Ansatz schon \(x'(t)\) und \(y'(t)\) falsch.

---

Aber ist nicht sin(t)´ ---> cos(t) ? und cos(t)´ → - sin(t) ?

---

Du hast bei den Ableitungen die konstanten Faktoren \(a\) und \(b\) verwechselt.

---

ohh stimmmmt !!! dankee!

Answer 1

In deiner ersten Zeile muss es

1/2 • ∫  [ a • cos(t ) • b cos(t) + b • sin(t) • a sin(t) ] dt heißen.

Dann klappt es :-)