Extremwertaufgabe: Flächeninhalt eines Dreiecks innerhalb einer Ellipse Maximieren

Question

folgende Aufgabe bereitet mir Schwierigkeiten:

Einer Ellipse ist ein gleichschenkliges Dreieck mit möglichst großen Flächeninhalt F einzuschreiben. Wie sind die Maße zu wählen und wie groß ist die Fläche F, wenn die Dreiecksspitze im Scheitel der Ellipse liegen soll? Auf die Prüfung der hinreichenden Bedingung ist zu verzichten.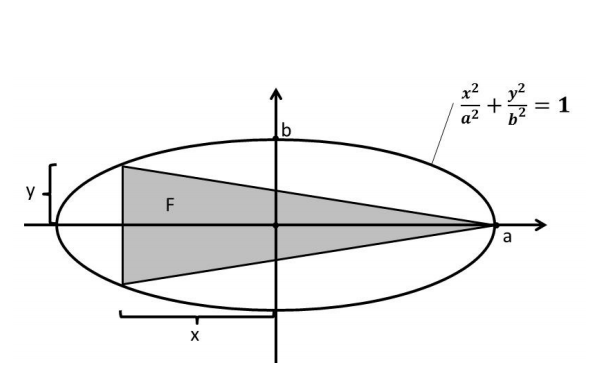

Das allgemeine Vorgehen ist ja: Zielfunktion aufstellen, ableiten, gleich 0 setzen. Jedoch finde ich hier leider keinen Ansatz.

Die Fläche eines gleichschenkligen Dreiecks wäre allg. (a*b)/2

Die Fläche F könnte man durch y*(x+a) (mit a ist die Differenz zwischen Ursprung und dem Punkt a gemeint) beschreiben.

Wie geht man nun weiter vor? Ist der Ansatz in die richtige Richtung?

Answer 1

Löse die Gleichung der Ellipse nach y auf. Wegen des y² bekommst du zwei Lösungen. Die eine beschreibt den Teil der Ellipse unterhalb der x-Achse, die andere den Teil oberhalb der x-Achse. Weil die Ellipse symmetrisch zur x-Achse ist, brauchst du nur den Teil oberhalb der x-Achse zu betrachten. Das ist deine Nebenbedingung.

Zielfunktion ist (weil das ja maximiert werden soll) der Flächeninhalt des Dreiecks. Dieser ist maximal genau dann wenn der Teil des Dreicks maximal ist, der oberhalb der x-Achse liegt. Dieser Teil ist ein rechtwinkliges Dreieck, dessen Flächeninhalt also die Hälfte des Produkts der Katheten.

> Die Fläche eines gleichschenkligen Dreiecks wäre allg. (a*b)/2

Was ist denn dann a und was ist b?

Answer 2

y*(x+a) ist richtig    und dann ist  die Ellipsengleichung die Nebenbedingung,

also etwa    y = b*√( 1 - x^2 / a^2 ) einsetzen gibt

A(x) =    b*√( 1 - x^2 / a^2 ) *(x+a) 

         =  (x+a) * √( b^2 - x^2 )    (neg. kann ja nicht sein.)

A ' (x) = √( b^2 - x^2 )  -    x*(x+a) / √( b^2 - x^2 )   

gleich 0 gesetzt bekomme ich  x =    (   - a  ±   √( 8*b^2  +a^2 )    / 4

Answer 3

Benenne einen Eckpukt des Dreiecks, der nicht auf einer Achse liegt, mit (r/s) Dann ist die Fläche des Dreiecks (1) F=s·(r+a). Die Nebenbedingung lautet (2) r²/a²+s²/b²=1. (2) nach s auflösen und in (1) einsetzen.