uneigentliches integral lösen

Question

Hallo

Ich soll das uneigentliche integral bestimmen.

Habe auch schon einen ansatz aber irgendwie komme ich in einen zyklus von produktintegrationen und komme deswegen nicht weiter. Hoffe ihr könnt mir da weiter helfen.

Comments

Lautet die Aufgabe wirklich so? Kann ich mir nicht vorstellen.

Dann müßtest Du ja 7 Mal partiell integrieren???

---

Ja leider

Aufgabenstellung: Berechnen Sie das folgende uneigentliche Integral.

---

Ich kann es nicht ganz genau lesen.

lautet die Aufgabe so?

---

256e^{-2x^2} * x(^15)

---

bleibt trotzdem bei 7 Mal partiell integrieren . Ergbnis:2520

Wer stellt denn solche Aufgaben??

---

dies ist eine alte klausuraufgabe gewesen kannst du mir deinen rechenweg bitte zeigen.

mfg

Answer 1

ich glaub es immer noch nicht , wer stellt solche Aufgaben?

Vielleicht ist dort ein Druckfehler in der Aufgabe, wenn nicht schon mal ein Anfang

Viel Spaß :-)

Answer 2

Tipp: Zeige per Induktion über \(n\) mit partieller Integration, dass für \(n\ge0\) gilt$$\int_0^\infty x^{2n+1}\cdot e^{-2x^2}\,\mathrm dx=\frac{n!}{2^{n+2}}.$$

Answer 3

2 Lösungsmöglichkeiten:

a) zig mal partiell Integrieren ist nicht komplett nötig, da bei Grenzen von 0 und ∞

sich ein Polynom ohne Offset nicht ändert: P(0) = 0 ; P(∞)=∞

Nur Offset am Ende ist interessant bei x^n im Integral:

n | Integral aufgelöst

1 | e^{-2x²}*(P()-1/4)

3 | e^{-2x²}*(P()-1/8)

5 | e^{-2x²}*(P()-2/16)

7 | e^{-2x²}*(P()-6/32)

9 | e^{-2x²}*(P()-24/64)

11 | e^{-2x²}*(P()-120/128)

13 | e^{-2x²}*(P() - 720/256)

15 | e^{-2x²}*(P() - ((n-1)/2)!/2^ ((n-1)/2+2) )

für n=15 ergibt sich Offset 315/32

e^{-∞}=0 und e^{0}=1

Faktor 256 noch dazu mit den Grenzen:

Integral=[0] - [1*-315/32]*256=2520

b) einige Bücher & Seiten wie

http://www.lamprechts.de/gerd/Integral_Substitutionen.html

§D4 bieten bereits fertige universelle Lösungen für beliebiges n an:

mit a=b=2 und n=15 ergibt das Integral

2^{-16/2}*Gamma2(8,2*x²)/(-2)

mit Faktor 256 und dazu Grenzen:

für diese Betrachtungen reicht die asymptotische Näherung

Gamma2(x,y)=(y^{x - 1}*hyg2F0[{1, 1 - x}, -(1/y)])/e^y  {hyg2F0()=hypergeometr. Funktion}

also Gamma2(x,∞)=0 , denn lim x^n/e^x ,x->∞=0

Gamma2(8,0)=5040 siehe Bild

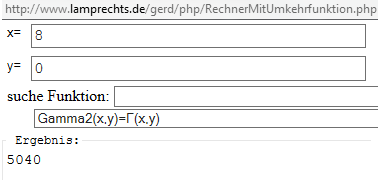
also

Integral=[0]-[-5040/2/2^8]*256

=5040/2=2520

Comments

Was heist denn? p()-1/4

---

nah wie im Satz darüber beschrieben "Polynom ohne Offset".

also mit beliebigen Faktoren und Potenzen

hätte besser P(x) schreiben sollen.

---

kleiner Schönheitsfehler:

[1*-315/32] sollte exakter sein: [1*(0-315/32)] 

und noch ein Hinweis, warum ein beliebiges Polynom ohne Offset durch e^x gegen 0 geht:

 lim xⁿ/e^x ,x->∞=0 , da Exponentialfunktion immer schneller wächst als jedes beliebige Polynom