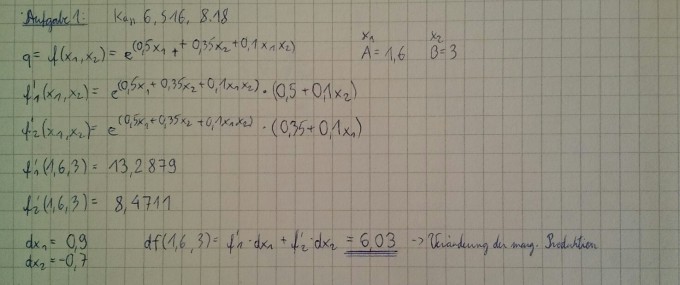Ich bitte umeiner Kontrolle meiner Berechnungen. Danke
Ein Unternehmen stellt ein Gut aus zwei Rohstoffen A und B her. Die herstellbare Menge des Gutes hängt ab von den Mengen an eingesetzten Rohstoffen gemäß der Produktionsfunktion
q=f( x1 , x2 )= e0.5 x1 +0.35 x2 +0.1 x1 x2
Dabei bezeichnen x1 und x2 die eingesetzten Mengen der Rohstoffe A und B und q=f( x1 , x2 ) die hergestellte Menge des Produkts. Zurzeit stehen 1.6 Tonnen des Rohstoffs A und 3 Tonnen des Rohstoffs B zur Verfügung. Es besteht die Möglichkeit, die Zulieferung des Rohstoffs A um 0.9 Tonnen zu steigern, während die Zulieferungen des Rohstoffes B in Zukunft um 0.7 Tonnen sinken werden.
Wie wird sich die marginale Produktion durch die veränderten Zulieferungen verändern?