Hallo ich habe Folgende Aufgabenstellung gegeben (Bild) : Es gilt zu Zeigen: 1) das die Folge an konvergiert .Und 2) man soll (falls möglich) den Grenzwert bestimmen.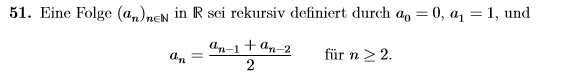
Für Konvergenz ist einerseits Monotonie und beschränktheit nötig.
Monotonie kann man sich die ersten Folgenglieder aufschreiben und eine vermutung aufstellen das die Folge zb bei allen geraden Indezes monoton steigt und bei allen ungeraden indezs monoton fallend.Das ist aber nicht eindeutig wenn nicht alle Folgenglieder steigen oder fallen.
Bei Beschränktheit fällt mir ein wenn also die 2 Teilfolgen die aus geraden und nichtgeraden Indezes bestehen sich mit sicherheit jeweils einem Gw annähern und somit besitzen sie auch eine Obereund untereSchranke.
Jedoch wie zeigt man das?. bzw. gibt es andere Vorschläge bzw. Ideen diese Aufgabe effizienter zu lösen?
Den Grenzwert vermute ich bei 2/3 .Ich habe mir eine explizite formel aufgestellt die lautet an=[2^n -(-1)^n]/(3*2^{n-1}] der Zähler bildet dabei eine Rekursionsformel für die Jacobszahlen und der Nenner einfach darauf angepasst.