Normierte Ricatti-Gleichung und skalare lineare DGL 2.Ordnung, Ähnlichkeit zeigen

Question

Gegeben seien die normierte Ricatti-Gleichung

z'(t) = -z²(t) + ĥ(t) * z(t) + ĉ(t)                  (1)

und die skalare lineare DGL zweiter Ordnung

x''(t) =  ĥ(t) * x'(t) + ĉ(t) * x(t)                    (2)

Zeigen Sie dass die beiden Gleichungen im folgenden Sinn äquivalent sind:

a) Falls φ: J→ℝ eine Lösung von (1) ist, so ist

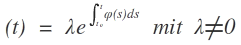
eine Lösung von (2)

b) Falls ψ:  J→ℝ eine Lösungvon (2) ist, die zusätzlich (t) ≠ 0 für alle t ∈ J erfüllt, so ist

 

eine Lösung von (1)

Answer 1

Hi, zu (a) sei
$$ \psi = \lambda \int_{t_0}^t \varphi(s) ds $$ mit \( \varphi \) Lösung von
$$  (1) \quad \varphi' = -\varphi^2 + h\varphi +c $$ dann gilt
$$  \psi' = \psi \varphi $$ und $$ \psi'' = \psi' \varphi + \psi \varphi' = \psi^2 \varphi + \psi(-\varphi^2 + h\varphi + c) = h\psi' + c\psi  $$ also ist \( \psi \) Lösung von
$$ (2) \quad x'' = hx' + cx  $$
Zu (b) Sei $$ \varphi = \frac{\psi'}{\psi}  $$ und \( \psi \) Lösung von (2) dann folgt
$$ \varphi' = \frac{\psi'' \psi - \psi'^2}{\psi^2} = \frac{(h \psi' + c\psi) \psi - \psi'^2}{\psi^2} = h\varphi+c - \varphi^2  $$
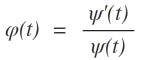
Also ist \( \varphi \) Lösung von (1)