a) Da die Aufgabe zeichnerisch zu lösen ist, musst du natürlich erstmal die beiden Punkte und eine Gerade durch sie zeichnen.
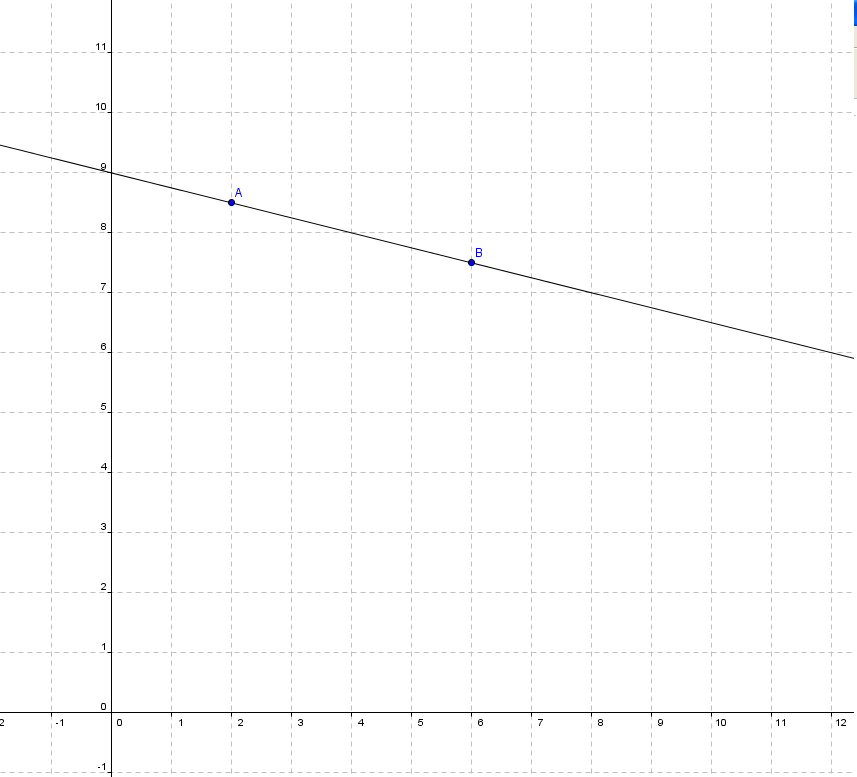
Jetzt kann man die Funktionsgleichung folgendermaßen ablesen:
Die Gleichung lautet (allgemein formuliert) f(x) = mx + n
Das n ist der y-Achsenabschnitt, also der Wert des Schnittpunkts mit der y-Achse. Der ist hier 9.
Das m kannst du zeichnerisch aus einem Steigungsdreieck ermittelt, indem du schaust, wieviel Schritte der Graph nach oben geht, wenn du einen Schritt nach rechts gehst. In diesem Fall folgt m = -1/4
Die Gleichung lautet also:
f(x) = -1/4 x + 9
b) Um den Schnittpunkt mit der x-Achse zu bestimmen muss f(x) = 0 gesetzt werden:
0 = -1/4 x + 9 | +1/4 x
x/4 = 9 | * 4
x = 36
Der Schnittpunkt lautet also (36, 0).
c) Die nächste Funktion (nennen wir sie g) hat wieder die allgemeine Form einer linearen Funktion:
g(x) = o*x+p
Ich habe andere Buchstaben gewählt, um sie von den Variablen des ersten Aufgabenteils zu unterscheiden.
Die Funktion geht durch den Nullpunkt, also gilt f(0) = 0 ⇒ p = 0
Außerdem soll sie die Steigung 2 haben ⇒ o = 2
Die Gleichung lautet also:
g(x) = 2x
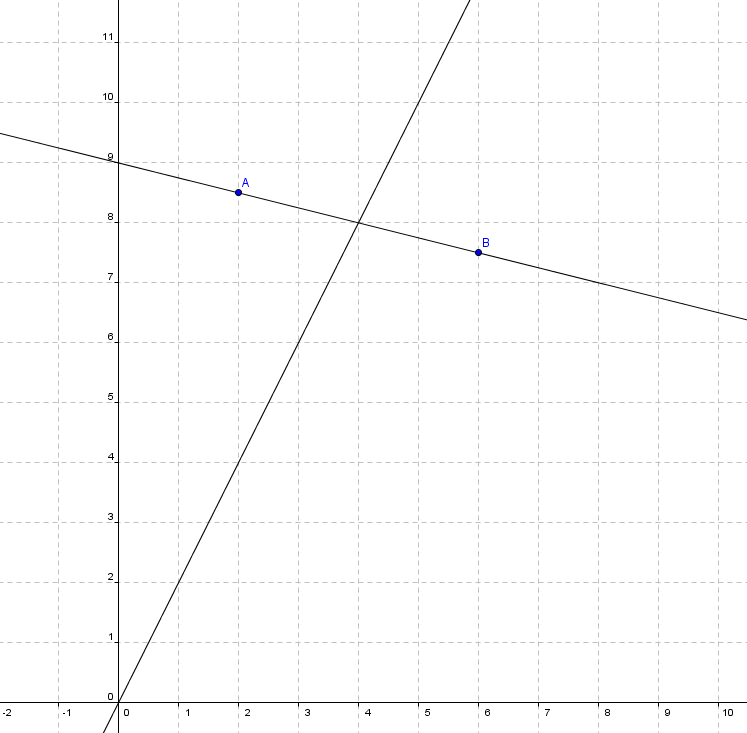
Und so sieht das gezeichnet aus.
d) Aus der Zeichnung lässt sich als Schnittpunkt der Punkt (4, 8) ablesen.
Rechnerische Prüfung:
für den Schnittpunkt gilt f(x) = g(x):
-x/4 + 9 = 2x | *4
-x + 36 = 8x | +x
36 = 9x | :9
4 = x
Eingesetzt in eine der Funktionsgleichungen ergibt sich dann auch hier der Punkt (4, 8).