Die Funktion schließt mit der x-Achse ein endliches Flächenstück ein.

Question

Gegeben ist die Funktion f(x) = x^2/4 - x/4 - 3

Die Funktion schließt mit der x-Achse ein endliches Flächenstück ein. Berechne dessen Inhalt. Berechne auch den Extremwert der Funktion und gib an, ob es sich um einen Hoch- oder Tiefpunkt handelt.

Bitte, wer hilft?? Danke.

Answer 1

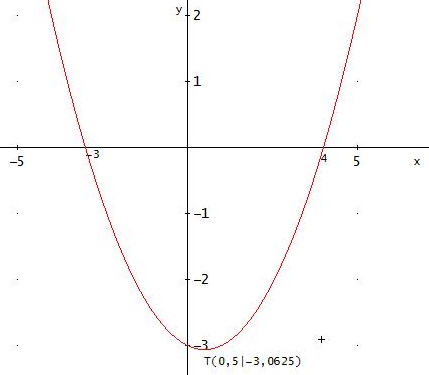
die  nach oben geöffnete Parabel  hat die Nullstellen  x₁ = 4 und  x₂ = -3

Fläche A = | ∫_-3⁴ f(x) dx |  =  | [ 1/12 • x³ - 1/8 • x² -3x ] _-3⁴  |  =  | - 343/24 |   ≈ 14,29

Diese Parabel hat nur einen Tiefpunkt . Dessen x-Wert erhältst du, indem du die erste Ableitung = 0 setzt:

f '(x) = 1/2•x - 1/4 = 0   →  x_T = 1/2   →  T(1/2 | -49/16) = (1/2 | - 3,0625)

Gruß Wolfgang