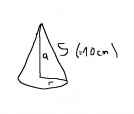Kegel Aufgabe (Extremalproblem)

Question

Wie müssen Grundkreisradius und Höhe gewählt werden, damit der Kegel maximales Volumen hat ?

S ("Mantellinie" ) 10 cm

Es folgt die Rechnung die ich vom Mathelehrer abgeschrieben habe, diese Verwirrt mich jedoch und ich bitte euch das ganze nochmal zu kontrollieren.

Hauptbedingung : V = π*r^2*h / 3

Nebenbedingung : 10 = √r^2*h^2 -> 100 = r^2*h^2

ERSTE FRAGE: Stimmt das so mit der Nebenbedinung ? Wenn ich die Wurzel ziehe wäre das dann nicht r*h = 100 ?

Oder versteh ich das komplett falsch ?

Weiter gehts: -> daraus folgt r^2 = 100/h^2

Zielfunktion: V (h) = π*(100-h^2)*h / 3

ZWEITE FRAGE: Wie bitteschön kommt der Lehrer jetzt auf 100 - h^2 für r^2 ?! Hieß es vorher nicht r^2=100 / h^2 ?

V'(h) = 100 π -3πh^2

DRITTE FRAGE: Wurde jetzt die 3 im Nenner erinfach weggelassen ? Kann man das so immer machen ?

0 = -100π / 3π + h^2

h = 5,77

VIERTE FRAGE: Wie bitte kommt man den jetzt auf "0 = -100π / 3π + h^2" -.-

100 - (5,77)^2 = r^2

8,16 = r

Vmax = 403,32

FÜNFTE FRAGE: Hier wieder. Warum 100 - ( 5,77 )^2 = r^2. Ich dachte r^2 = 100 / h^2

Hab wohl leider doch mehr Probleme als gedacht- vorallem beim Umformen, vorallem wenn die Aufgabe vom Lehrer richtig ist, aber vielleicht ist die ja falsch und der Lehrer hat Mist gebaut.

Ich schreibe morgen eine Klausur über ( unter anderem ) diesem Thema.

Wenn ihr mir Übungen für das Umformen mit π und r und h blablabla geben könntet ( mit Lösungen ) wäre ich ebenfalls dankbar.

Answer 1

Hallo

1.

Für die Mantellinie gilt nicht

$$ 10=\sqrt{r^2 \cdot h^2} $$

sondern

$$ 10=\sqrt{r^2+h^2} $$

Das ergibt sich aus dem Satz des Pythagorags. Ich denke, das hast Du ggfs. falsch abgeschrieben. Das erklärt dann auch später

2.

$$ r^2 = 100-h^2 $$

3.

Wie die Umformung der Zielfunktion V(h) zu V'(h) funktioniert, verstehe ich allerdings auch nicht. Richtig wäre:

$$ V(h) = \pi \cdot (100-h^2) \cdot h \cdot \frac{1}{3} $$

$$ V(h) = \frac{100}{3} \pi h - \pi \frac{h^3}{3} $$

$$ V'(h)= \frac{100}{3} \pi - \pi h^2 $$

4.

V' wird hier gleich 0 gesetzt um den Extrempunkt zu ermitteln.

5.

Hier gilt wieder, dass Deine Annahme zur Mantellinie falsch ist.

Gruß

Comments

Ich check das umformen von V(h) nicht und auch nicht wie du auf die Ableitung kommst :D Alter ist das hardcore. 

Hast du mal gecheckt ob bei dir für h = 5,77 rauskommt ? ( Ist richtig ). Ich wollte das gerade für deine erste Ableitung ausprobieren,weiß allerdings nicht wie ich das für h =... umstelle :D ohje...

---

Das Umformen von V(h) habe ich gerade bei der anderen Antwort erläutert. Zum Ableiten stell Dir einfach vor oder ersetze einfach konkret jedes h durch ein x. Dann mit den gewohnten Regeln nach x ableiten. 

$$ V(x) = \frac{100 \pi}{3} \cdot x - \frac{\pi }{3} x^3 $$

$$ V'(x) = \frac{100 \pi}{3} \cdot 1 \cdot x^{1-1}  - \frac{\pi }{3} \cdot 3 \cdot x^{3-1} $$

$$ V'(x) = \frac{100 \pi}{3} \cdot x^{0}  - \frac{\pi \cdot 3}{3} \cdot x^2 $$

$$ V'(x) = \frac{100 \pi}{3} \cdot 1  - \frac{\pi }{1} \cdot x^2 $$

$$ V'(x) = \frac{100 \pi}{3}   - \pi x^2 $$

Extremstelle V'(x)=0

$$ \begin{aligned} 0 &=& \frac{100 \pi}{3}   - \pi x^2 &&\qquad \vert : \pi \\ 0 &=& \frac{100}{3}   -  x^2 &&\qquad \vert -x^2 \\ x^2 &=& \frac{100}{3} &&\qquad \vert \sqrt{} \\ x &=& \pm \sqrt{\frac{100}{3}} \end{aligned} $$
Die negative Lösung ist nicht interessant, da die Höhe nicht negativ sein kann. Daher

$$x=h= \sqrt{\frac{100}{3}}=\frac{10}{\sqrt{3}} \approx 5,77 $$
Gruß

---

Dankeschön für die ausführliche Erläuterung.

Answer 2

NB: r^2 + h^2 = 100 --> r^2 = 100 - h^2

HB: 

V = 1/3·pi·r^2·h

V = 1/3·pi·(100 - h^2)·h = 100·pi·h/3 - pi·h^3/3

V' = 100·pi/3 - pi·h^2 = 0 --> h = √(100/3) = 5.774

Comments

ZWEITE FRAGE: Wie bitteschön kommt der Lehrer jetzt auf 100 - h² für r² ?! Hieß es vorher nicht r²=100 / h² ?

Der Satz des Pythagoras lautet a^2 + b^2 = c^2

DRITTE FRAGE: Wurde jetzt die 3 im Nenner erinfach weggelassen ? Kann man das so immer machen ? 

Konstante Faktoren die die Gesamte Funktion betreffen, ändern nichts am Maximum oder Minimum und können weggelassen werden.

VIERTE FRAGE: Wie bitte kommt man den jetzt auf "0 = -100π / 3π + h²" -.-

Die Ableitung des Volumens gleich 0 setzen.

---

zur Dritten Frage:

Es ist korrekt, dass Faktoren, die die gesamte Funktion betreffen, nichts an den Extremstellen derselben ändern, aber hier steht V'(h)= ... und das entspricht so aber nun einmal nicht V', oder? Hinzu kommt, dass man dann auch das π direkt mit weglassen könnte.

Gruß

---

Danke für deine Erläuterung. Aber kannst du mir eins näher erklären ?

V = 1/3·pi·(100 - h²)·h = 100·pi·h/3 - pi·h³/3

Wie genau kommst du auf 100·pi·h/3 - pi·h³/3. Also in Einzelschritten. Kann ich nicht nachvollziehen.

Und wie genau leitest du ab ? Auch das kann ich nicht richtig nachvollziehen. Ich hab echt Schwierigkeiten bei sowas ._.

---

Du musst einfach ausmultiplizieren:

$$ V = \frac{\pi}{3} ( 100 - h^2) \cdot h = \frac{\pi}{3} \cdot h \cdot ( 100 - h^2)  $$

$$ = \frac{\pi h}{3}( 100 - h^2) = 100\cdot  \frac{\pi h}{3} - \frac{\pi h}{3} \cdot h^2 $$

$$ = \frac{100\pi h}{3} - \frac{\pi h \cdot h^2}{3} =  100 \pi \cdot \frac{h}{3} - \pi \frac{h^3}{3} $$

Gruß

Answer 3

Hier einmal die Berechnungen Schritt für Schritt

Und noch der Radius

10^2 = r^2 + h^2
100 - 5.77^2 = r^2
r = 8.17

mfg Georg