Stetigkeit bestimmen von f(x):= x² + 2x für x ≤ 2 ; f(x):= 1,5 x² für x > 2

Question

Die Stetigkeit bestimmen von
f(x) = x² + 2x für x ≤ 21,5 x²   für x > 2
und

f(x) = x² -x für x ≤ 1
In x  für x > 1  

Danke

Answer 1

Die Stetigkeit bestimmten von 
f(x) = x² + 2x für x ≤ 2           1,5 x²   für x > 2

Stetigkeit bei geteilten Funktionen bedeutet :
( einfache Definition, für diese Aufgabe )
hat die geteilte Funktion an der Nahtstelle denselben Funktionswert ?
f(x) = x² + 2x für x ≤ 2        
f ( 2 ) = 2^2 + 2*2
f ( 2 ) = 8

f ( x) =  1,5 x²   für x > 2
f ( 2 ) = 1.5 * 2^2
f ( 2 ) = 6

Die Funktionswerte sind nicht gleich.
Die Funktion ist nicht stetig.


Schaffst du die andere Aufgabe ?

Comments

Super! Danke. Deine Erklärung hat mir sehr geholfen.

Answer 2

 

allgemeiner gilt:

am Beispiel von

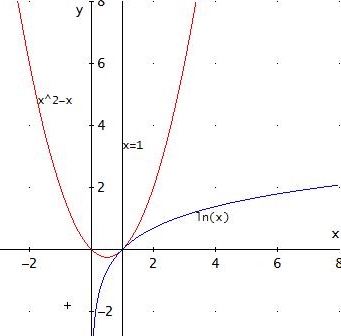
f(x) = x² - x  für x≤1

ln(x)    für x>1

lim_x→1-  f(x) = lim_x→1- (x² - x) = 0   und  lim_x→1+  f(x) = lim_x→1+  ln(x) = 0

 →   lim_x→1 f(x)  = 0 = f(1)

Eine Funktion ist stetig an der Stelle x₀ ∈ D, wenn im_x→xo  f(x) = f(x₀)

Da f in ℝ\{1} (ggf.) als Kompositon stetiger Funktionen stetig ist, ist f in ℝ stetig.

 Für x≤1 gilt der Graph von x²-x, für x>1 der von ln(x). Die beiden "Graphenteile" stoßen in x=1 aneinander,

was anschaulich Stetigkeit bedeutet:

Gruß Wolfgang und frohe Weihnachten