Nachfragefunktion erstellen

Question

Wie kann ich aus diesen Daten eine Nachfragefunktion erstellen? Bin gerade voll überfordert mit diesen Daten.

Preis	Menge
14,44	33
13,81	69
12,48	145
11,675	191
11,3425	210
9,3475	324
8,3675	380
6,5825	482
6,285	499

Answer 1

p(x) = (6.285 - 14.44)/(499 - 33)·(x - 33) + 14.44 = 15.0175 - 0.0175·x

Da die Funktion aus dem ersten und dem letzten Wert aufgestellt worden sind solltest du die mittleren Werte mal prüfen ob die alle so stimmen.

Answer 2

Die exakte Funktion "Preis von Menge" lautet:

p(x)=2.786084491e-6*sqrt(x)+15.01748563-1.750009821e-2*x

mit sqrt= Wurzel und 1.750009821e-2 = 0.01750009821

Der Iterationsrechner zeigt das bei Rundung auf 4 Stellen alles stimmt:

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#-1.750009821e-2*x+2.786084491e-6*@Qx)+15.01748563@NaB=Array(33,69,145,191,210,324,380,482,499);@N@Ci]=round(Fx(@Bi])*1e4)/1e4;@Ni%3E8@N0@N0@N#

Praktisch etwas unlogisch, wenn Preis bei mehr Stück ansteigt...

Falls Ihr erst lineare Regression hattet, kannst Du den Wurzel-Teil weglassen.

Comments

Ich verstehe nicht wie sie auf diese Nachfragefunktion gekommen sind.
Könnten Sie vielleicht etwas präziser werden?

Warum stimmt Ihrer Meinung nach die Antwort des Mathechoaces nicht.

:)
lg.

---

Ich habe nie gesagt, dass die andere Rechnung nicht stimmt. Wie man per Iterationsrechner sieht:

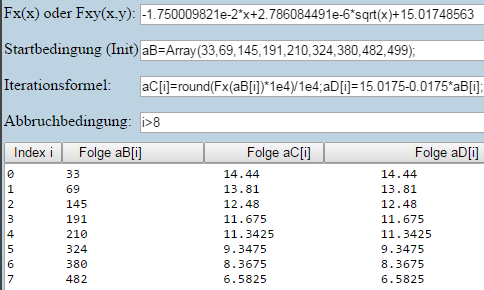
stimmen beide Formeln (also Spalten) auf 4 Stellen überein.

Er hat einfach eine Geradengleichung aufgestellt und dabei nur 1. und letzten Punkt betrachtet.

Das kann man nur machen, wenn man absolut sicher ist, dass alle Punkte dazwischen auch absolut linear sind.

Ich habe dagegen alle Punkte betrachtet und eine universelle nichtlineare Regression durchgeführt.

Da Ihr vermutlich noch nie was mit nichtlinearer Regression hattet und "Nachfrage" meist linear ist, kann mein winziger Einflußfaktor (2.786084491e-6*Wurzel(x) verändert in diesem Bereich nur die 6. Nachkommastelle) weggelassen werden.

Genau das meinte Mathecoach ja auch mit "mal prüfen ob die alle so stimmen" -> und da alle stimmen, wäre eine nichtlineare R. nicht nötig gewesen.

Ich zeige einfach gern, dass mehrere Wege zum Ziel führen und nehme dabei immer den universelleren. (In der Physik gibt es mehr nichtlineare Vorgänge)

---

Vielen herzlichen Dank!
Sie haben mir echt weitergeholfen.

---

Das Problem wäre das man in der Natur eventuell Messfehler haben kann und dann eine Funktion die ganz exakt ist eventuell sogar kontraproduktiv ist.

Daher ist es immer günstig sich die Gegebenen Werte zu anfang zu zeichnen, dann eventuell einen Ansatz zu vermuten. Der wäre hier linear. Ich habe den gleich linear gewählt weil Preisfunktionen üblicherweise lineare Funktionen sind.

Und anhand des Ansatzes dann eine Funktion zu modellieren. Dabei ist es nicht wichtig das die Funktion ganz exakt alle Werte wiedergibt, sondern meist das das Modell stimmt. Was sind da schon Abweichungen von unter 0.1%. Wer kann in der Realität schon auf 0.1% genau messen?