Maximum der Funktion f(x,y)=xy(4c-x-y) auf D berechnen

Question

Es sei \( c>0, D=\left\{(x, y) \in \mathbb{R}^{3}: x, y \geq 0, x+y \leq 4 c\right\} \) und
\( f(x, y)=x y(4 c-x-y) . \)

Bestimme den größten Wert von \( f \) auf \( D \).

Tipp: Berechne zunächst die Werte von \( f \) auf dem Rand von \( D \) und folgere, dass \( f \) das Maximum im Inneren von \( D \) annimmt.

Soll ich hier f ' (x) und f ' (y) ausrechnen? und dann schauen ob das im Definitionsberech gilt?

Answer 1

f(x,0)=x0(4c-x-0) =0

f(0,y)=0y(4c-0-y) =0

f(x,4c-x)=x(4c-x)(4c-x-(4c-x)) = x(4c-x)(0) = 0

Fazit: Auf dem Rand ist der Funktionswert immer 0.

Im Innern des Dreiecks liegt z.B. (c,c)

f(c,c)=cc(4c-c-c) = 2c^3                   Dieser Funktionswert ist n.V. grösser als 0.

Da die Funktion stetig und nicht immer 0 ist, liegt im angegebenen Bereich sicher ein lokales Maximum.

Ausserhalb des Dreiecks sind wohl 1 oder 3 Faktoren des Produkts negativ. Am besten zeichnest du das auf um zu begründen, dass nur 2 Faktoren negativ unmöglich ist.

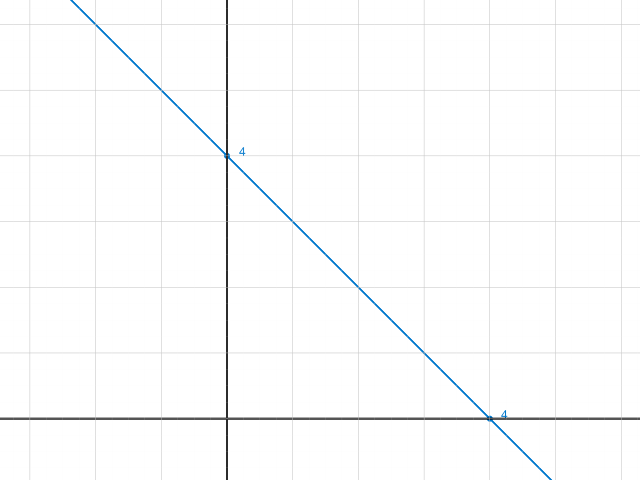
Hier die Skizze für c=1. Wenn du eine allgemeine Skizze brauchst, schreibst du statt 4 einfach 2 mal 4c an die Achsen.