Warum ergibt cos x * tan x gleich sin x?

Question

Wie lautet der Beweis für:

cos x * tan x = sin x

?

Answer 1

ergibt sich aus den Beziehungen der Kreisfunktionen

 der tan α =sin α/cos α   ⇒tan α * cos α =sin α

(strahlensätze, verhälnisse zahlen)

Siehe Video über die Kreisfunktionen bei matheretter.de

Siehe Skizze:

Answer 2

Ich sehe nicht so richtig, wie die Skizze da weiterhilft, da das Produkt von Strecken im Bereich der reellen Zahlen keine sinnvolle Interpretation besitzt. (Betrachtet man den Einheitskreis in der komplexen Zahlenebene, dann kann man das Produkt von zwei komplexen Zahlen so interpretieren, dass die Winkel addiert und die Beträge malgenommen werden, sodass sich eine Multiplikation dann als Drehung und damit einhergehende Streckung beschreiben lässt, allerdings ist das wohl ein bisschen zu kompliziert :-))

 

Einfacher finde ich den Beweis über die Definitionen der Winkelfunktionen im rechtwinkligen Dreieck. Nehmen wir mal an, wir haben ein rechtwinkliges Dreieck mit den Seiten a, b und c.

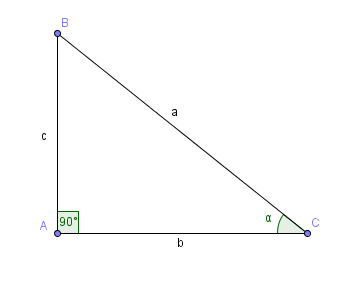
Jetzt sind die Winkelfunktionen für den Winkel α folgendermaßen definiert:

sin α = c/a ( "Gegenkathete durch Hypotenuse")

cos α = b/a ( "Ankathete durch Hypotenuse")

tan α =  c/b ("Gegenkathete durch Ankathete")

Also:

cos α * tan α = b/a * c/b = c/a = sin α

Comments

Akeleis Antwort ergibt sich aus dem Strahlensatz. Diese Beziehung in den Kreisfunktionen ergibt sich aus deren Definition am Einheitskreis. Dein Beweis ist natürlich ok für alle Alpha bis 90°.

---

Ah, okay, das kann ich nachvollziehen.
Trotzdem wäre dann vielleicht ein klärender Satz dazu noch ganz hilfreich, nur das Stichwort "Strahlensatz" hilft da mMn nicht so richtig weiter.

---

Ja. Die beiden parallelen Geraden sind ja in der Skizze auf unterschiedlicher Seite des Schnittpunkts der Strahlen.

---

wenn man die Skizze (Strahlensatz) etwas umformt, so dass das Dreieck mit sin und cos im Dreieck (tan) liegt,
dann sieht man auf Grund der "Ähnlichkeit von Dreiecken" [ Seite, Winkel (90°), Seite] das Verhältnis: Sin ist zu cos wie tan zu eins ( im Einheitskreis ist der Radius gleich 1,so auch in der Skizze dargestellt.)