Konvergenzradius von Potenzmengen

Question

 

und zwar ich weiß, dass man Konvergenzradien folgender Maßen löst:

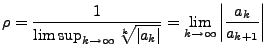
a) 

ich habe folgendes verwendet: 

lim |ak/ak+1| = lim |1/nⁿ/1/(n+1)ⁿ⁺¹|

= lim | n+1ⁿ⁺¹/nⁿ|

= lim |(n+1)*(n+1)ⁿ /nⁿ| 

= lim 1/nⁿ * (n+1) * (n+1)ⁿ 

1/nⁿ geht gegen 0 und dadurch, dass alles mal 0 multipliziert wird ergibt es:

r=0

Stimmt das?

Und irgendwie komme ich bei den anderen nicht voran! Würde mich sehr über Hilfe freuen ! :)

Comments

b)

an/an+1

= n!^2/(2·n)!·z^n / ((n + 1)!^2/(2·(n + 1))!·z^{n + 1})

Aufschreiben und dann vereinfachen soweit es geht. Das musst du tatsächlich selber machen.

= 2·(2·n + 1)/(z·(n + 1))

lim n --> ∞

= 4/z

Wenn du im Besitz von Wolframalpha Fürs Smartphone oder Tablet bist, kann der dir vermutlich auch dabei helfen. Sogar mit Schritt-Für-Schritt Lösung.

---

Was ergibt den der Grenzwert einer Fakultät?

---

Der Grenzwert einer Fakultät ist unendlich.

lim (n --> ∞) n! = ∞

Aber meist heben sich die Fakultäten ja recht gut weg, bis auf ein paar faktoren.

---

Bei der b) habe ich das= n!²/(2·n)!·zⁿ / ((n + 1)!²/(2·(n + 1))!·z^{n + 1}) auf
=(n!)^2(2+1)!z^n / (2n)!(n+1!)^2 z^{n+1} vereinfacht bin mir aber nicht sicher, ob das so stimmt.

Answer 1

zu a )  ich habe folgendes verwendet: 

lim |ak/ak+1| = lim |1/nⁿ/1/(n+1)ⁿ⁺¹|

= lim | n+1ⁿ⁺¹/nⁿ|

= lim |(n+1)*(n+1)ⁿ /nⁿ|    soweit ok, dann aber

= lim  (n+1) * ( (n+1)ⁿ     /  n^n  )

= lim  (n+1) *  (1+1/n)ⁿ   

Der 2. Faktor geht gegen e und der erste ist unbeschränkt, also GW + unendlich.

Das ist der Konv.rad.

Answer 2

die Dinger heißen Potenzreihen und nicht Potenzmengen. Den Konvergenzradius löst man nicht nicht, sonder man bestimmt ihn.

Deine Argumentation ist am Ende leider nicht mehr tragbar. Das ganze geht eigentlich gegen \(\infty\). Das kannst du wahrscheinlich mit dem Wurzelkriterium zur Bestimmung des Konvergenzradius besser nachvollziehen.

Gruß