Hallo , ich habe folgende Aufgabenstellung gegeben.
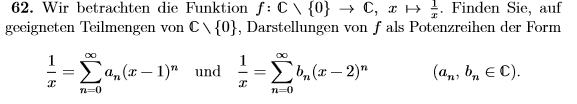
Ich habe mir gedacht die Geometrische Reihe zu verwenden. $$\sum _{ n=0 }^{ \infty }{ { q }^{ n } } =\frac { 1 }{ 1-q } $$ falls |q|<1 ist.
Meine Idee wäre den Ausdruck 1/x umzuformen auf $$\frac { 1 }{ 1-(x-1) } $$*Restterm und darauf die Formel Für die Geometrische Reihe Verwenden. Ich habe mit (2/x -1)/(2/x -1) erweitert , sodass steht $$\frac { 1 }{ 1-(x-1) } *\left( \frac { 2 }{ x } -1 \right) $$ . Für den Term auf der linken seite Könnte ich nun die geometrische Reihe benutzen . aber wie gehts weiter ? was passiert mit dem Rechten Term? bzw. passt das was ich mir überlegt habe?
Bitte um eine Antwort . Danke !