folgende Aufgabe ist gegeben:

Antworten zu:
(a)
• DB:{x∈ℝ:x>0}
• f(x) ist stetig auf DB, da man die Funktion ohne abzusetzen zeichnen kann.
(b)
$$0=\frac { ln({ x }_{ 0 }) }{ { x }_{ 0 } } ⇒{ x }_{ 0 }=1$$
(c)
$$\underset { x\rightarrow 0 }{ lim } \frac { lnx }{ x } =\frac { -\infty }{ 0 } =-\infty \\ \underset { x\rightarrow +\infty }{ lim } \frac { lnx }{ x } =\frac { \infty }{ \infty } ={0} $$
(d)
$$(\frac { f }{ g } { ) }^{ ' }=\frac { f'\cdot g-g'\cdot f }{ { g }^{ 2 } } =\frac { \frac { 1 }{ x } \cdot x-lnx }{ { x }^{ 2 } } =\frac { 1-lnx }{ { x }^{ 2 } } \\ (\frac { f }{ g } { ) }^{ '' }=\frac { f'\cdot g-g'\cdot f }{ { g }^{ 2 } } =\frac { -\frac { 1 }{ x } \cdot { x }^{ 2 }-(1-lnx)2x }{ { x }^{ 4 } } $$
(e)
$$max\quad \frac { 1 }{ e } \approx 0.37$$
Monoton fallend: x<1
Monoton steigend: x>1
(f)
$$\frac { lnx }{ x } \\ f(1)=0\\ f'(1)=1\\ f''(1)=-3\\ \\ y(x)=f({ x }_{ 0 })+f'({ x }_{ 0 })\cdot (x-{ x }_{ 0 })+\frac { 1 }{ 2 } \cdot f''({ x }_{ 0 })\cdot (x-{ x }_{ 0 }{ ) }^{ 2 }\\ y(x)=0+1\cdot (x-1)+\frac { 1 }{ 2 } \cdot (-3)\cdot (x-1{ ) }^{ 2 }\\ y(x)=(x-1)+(-\frac { 3 }{ 2 } )\cdot ({ x }^{ 2 }-2x+1)\\ y(x)=\quad (x-1)+(-\frac { 3 }{ 2 } { x }^{ 2 }+3x-\frac { 3 }{ 2 } )\\ y(x)=-\frac { 3 }{ 2 } { x }^{ 2 }+4x-\frac { 5 }{ 2 } $$
(g)
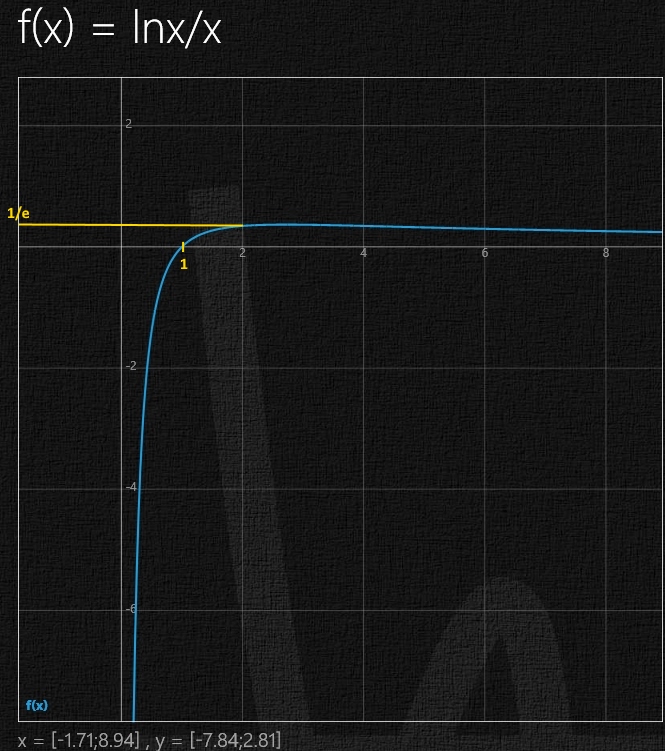
Wurde alles richtig berechnet oder haben sich Fehler eingeschlichen?
Beste Grüße,
Asterix