Welches Polynom 4-ten Grades hat im Ursprung einen Sattelpunkt...

Question

Aufgabe: Welches Polynom 4ten Grades hat im Ursprung einen Sattelpunkt, und schneidet die x-Achse bei x=8 mit einer Steigung von m=-8?

Komme bei dieser Aufgabe leider gar nicht weiter.

Ich vermute ich muss ein Gleichungssystem aufstellen anhand einer Gleichung 4. Grades, weiß aber nicht wie ich die Infos Sattelpunkt und Steigung darin verpacken soll.

Answer 1

Sattelpunkt bei (0;0) heißt

f(0) = 0

f '  (0) = 0

f ' ' (0) = 0

schneidet die x-Achse bei x=8 mit einer Steigung von m=-8

f (8) = 0

f ' (8) = -8

Dann hast du 5 Gleichungen, das langt.

Comments

danke :)noch eine kurze Frage fällt mir da ein. Habe letztens Extrema bestimmt, und dort gab eine Nullstelle der ersten Ableitung auch in der zweiten und dritten Ableitung 0, was liegt dann vor?

---

wenn dann die 4. Ableitung ungleich 0 ist, ist es ein Extremum.

Beispiel f(x) = x^4 .

Wenn zum  ersten mal eine  Abl. ungleich 0 ist das ist die n-te Abl.

dann ist es ein Extr.  , wenn n gerade und ein

wendepu. wenn n ungerade.

---

ist das Ergebnis der ersten Aufgabe f(x)=-1/64x^4+1/8x^3 ?

---

scheint zu stimmen

~plot~-1/64*x^4+1/8x^3;[[-1|10|-1|8]]~plot~

---

haben Sie mittlerweile eine Lösung ?

Answer 2

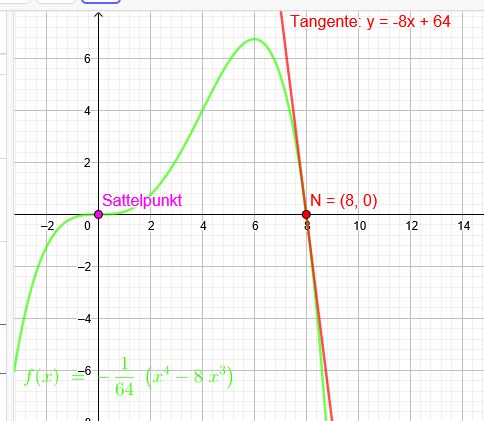
Welches Polynom 4. Grades hat im Ursprung einen Sattelpunkt und schneidet die x-Achse bei \(x=\red {8}\) mit einer Steigung von \(m=\green{-8}\)?

Im Ursprung Sattelpunkt bedeutet Dreifachnullstelle , schneidet die x-Achse bei \(x=8\) ( ist einfache Nullstelle)

\(f(x)=ax^3(x-8)=a(x^4-8x^3)\)

\(f'(x)=a(4x^3-24x^2)\)

\(f'(\red {8})=a(4\cdot 8^3-24\cdot 8^2)\)

\(a(4\cdot 8^3-24\cdot 8^2)=\green{-8}\)

\(a=-\frac{1}{64}\):

\(f(x)=-\frac{1}{64}(x^4-8x^3)\)