Polynomische Funktion 3. Grades nach x auflösen

Question

Hallo ich brauche Eure Hilfe,

da ich schon länger aus der Schule draußen bin, stehe ich vor nem kleinen mathematischen Problem.

Ich habe in einem Experiment Messwerte erhalten, die ich als Kalibirergrade nutzen möchte. Mit Excel habe ich mir die Regressionsgrade und die dazugehörige Gleichung erstellen lassen.

Um eine vernünftige Regression zu bekommen, habe ich eine polynomische Funktion 3. Grades gewählt. Excel hat mir nun folgende Gleichung ausgespuckt:

y= 0,038x³-0,432x²+0,9384x+2,1784  (mit R²=0,999)

Ich habe nun mehrere y-Werte und muss die dazugehörigen x-Werte ermitteln. Dabei entsprechen die y-Werte photometrisch gemessene Werte und die x-Werte entsprechende Konzentrationsangaben (nur am Rande erwähnt ;) )

Wie kann ich mit Hilfe der y-Werte ( zB. 0,65) die X-Werte ermitteln bzw. nach x auflösen. Dabei müsste jedem y-Wert genau einem x-Wert zugeordnet werden, da ja der photometrische Wert genau einer bestimmten Konzentration entsprechen muss.

Vielen Dank für Eure Hilfe

Comments

Um eine vernünftige Regression zu bekommen, habe ich eine polynomische
Funktion 3. Grades gewählt. Excel hat mir nun folgende Gleichung ausgespuckt:

y= 0,038x³-0,432x²+0,9384x+2,1784  (mit R²=0,999)

Du hast also Meßwerte ( x | y ) und konntest dir von Excel eine Funktion 3. Grades berechnen lassen.

Wenn du x und y vertauschst könntest du dir die Umkehrfunktion berechnen lassen.

Ansonsten kannst du die Meßwerte einmal hier einstellen und dann kann ich dir eine Funktion berechnen.

---

das sind meine Originalmesswerte. Die Konzentration [ng/ml] habe ich als x-Wert definiert. Die entsprechenden y-Werte gibt es einmal für ein Toxin A und einmal für Toxin B. Die y-Werte ergeben sich aus der gemessenen optischen Dichte, aber ich schätze das ist irrelevant.

Du hast also Meßwerte ( x | y ) und konntest dir von Excel eine Funktion 3. 
Grades berechnen lassen.

Genau, ich habe mir über Excel die Graphen und die Regression darstellen lassen.

Danke für deine Hilfe

---

Wichtig für mich ist, dass ich weitere X-werte aus vorhandenen y-werten berechnen kann

---

für mich zunächst einmal

~plot~ { 2.796| 20 } ; {2.724 | 10} ; {2.620 | 5 } ; { 2.171|2.5 } ; {1.417 |1.25 } ; {0.87 | 0.63} ; {0.495 | 0.31} ; [[ 0 | 3 | 0 | 21 ]] ;  ; tan ( 0.542 * x ) * 1.11 ~plot~

Answer 1

Hi, darfst du einem programmierbaren Taschenrechner verwenden? Wenn ja gebe die Funktion in dein Taschenrechner ein und löse nach x auf.Es gibt solche Befehle wie zum Beispiel "solve". Mit denen kannst du dann deine Funktion nach einen bestimmten Parameter auflösen.

Comments

Leider besitze ich so einen Taschenrechner nicht. Ideal wäre eine nachvollziehbare Umstellung nach x, sodass ich diese auch in Excel eintragen kann und der mir alle Werte automatisch (ohne Neueingabe) ausrechnet.

---

Die Umstellung ist mit richtig ungünstigen Zahlen vorhanden.  Das bekommt man nicht so schnell mit der Hand hin.  Ich würde mir einen Gleichungslöser im Internet suchen.  Dort kannst du das auch lösen.  Per Hand ist das so gut wie nicht schaffbar.

Als f (x) Wert nimmst du die optische Dichte.  Der Rechner soll dir dann nach x( Konzentration) lösen.

Hier ein Link:

https://de.numberworld.info/gleichungsLoeser

---

Danke für den Link. Habe ich gleich mal ausprobiert, aber leider auch nur eine weitere ellenlange Gleichung mit ner zusätzlichen Variablen i bekommen :(

---

Also i steht eigentlich für eine komplexe Zahl.  Das kann definitiv die Lösung nicht sein.  Versuche mal einen anderen Gleichungslöser im Internet zu finden. Ansonsten kann ich dir leider auch nicht mehr helfen.  Wenn es so nicht funktioniert weiß ich auch nicht mehr.  Sonst frage nochmal bei deinem Lehrer nach, ob er einen Tipp hätte.

Answer 2

Was hast Du denn da für eine Regression gemacht? Dieses Polynom 3. Grades liegt entweder völlig daneben, oder Du hast statt echter x-Stützstellen einfach 1,2,3,... eingesetzt ???

Um das mal zu zeigen mit "echten x Werten aus der Quell-Grafik":

Deine Kurve rot: 0.0382*pow(x,3)-0.4321*x*x+0.9384*x+2.1784

bestes Polynom Grad 3

grün 8.377712264e-3*pow(x,3)-0.1747566482*x*x+1.169964125*x+0.1764596151

meine Vermutung blau:(2.803942437*pow(x,1.93692701)+0.7316411079)/(pow(x,1.93692701)+1.936340944)

zusammen hier eingeben {x³ = x*x*x = x ^ 3 = pow(x,3)  }:

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

aB[0]<1?0.0382*pow(x,3)-0.4321*x*x+0.9384*x+2.1784:(aB[0]==1)?8.377712264e-3*pow(x,3)-0.1747566482*x*x+1.169964125*x+0.1764596151:(2.803942437*pow(x,1.93692701)+0.7316411079)/(pow(x,1.93692701)+1.936340944)

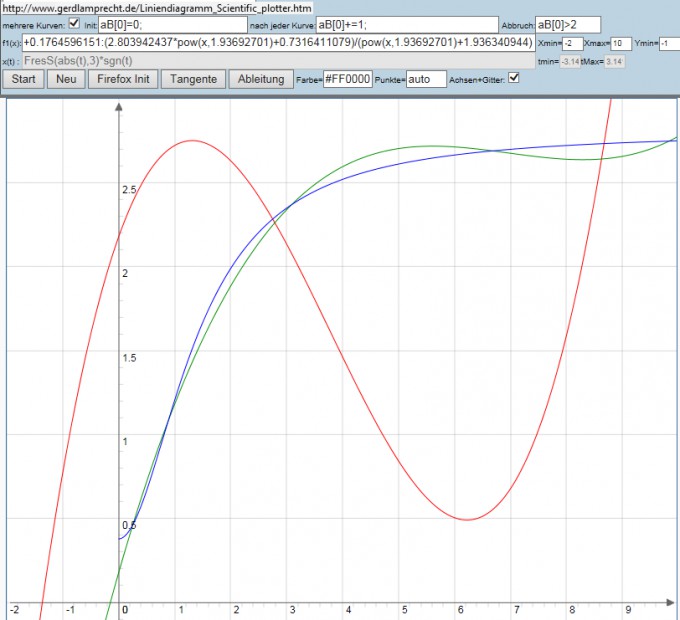
Nun kann man entweder mit Button "Tangente" (nur 1 Kurve und Punkte = auto) per Maus den Punkt anfahren und auf 2 Nachkommastellen ablesen

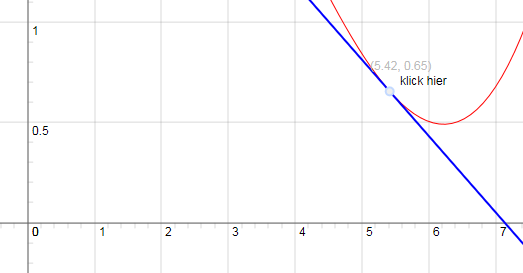
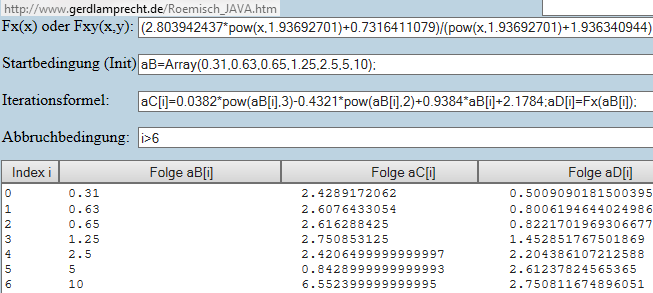
Oder per Iterationsrechner eine Wertetabelle anlegen (Spalte aC Deine;  aD mein Vorschlag blau):

http://www.gerdlamprecht.de/Roemisch_JAVA.htm#(2.803942437*@Px,1.93692701)+0.7316411079)/(@Px,1.93692701)+1.936340944)@NaB=Array(0.31,0.63,0.65,1.25,2.5,5,10);@N@Ci]=0.0382*@P@Bi],3)-0.4321*@P@Bi],2)+0.9384*@Bi]+2.1784;aD[i]=Fx(@Bi]);@Ni%3E6@N0@N0@N#

Oder je nach verwendeter Funktion die Umkehrfunktion bilden (exakter Weg).

Nun kenne ich Deine Fähigkeiten nicht, aber die PQRST-Formel für kubische Gleichungen 3. Grades hattest Du bestimmt noch nicht.

Für Deine Funktion (rot) und Vorgabe y= 0.65 bedeutet das eine Verschiebung Deiner Funktion um 0.65 Einheiten nach unten, also statt 2.1784 nun Offset (2.1784-0.65 = )  1.5284

was exakt die 3 Nullstellen ergibt:

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php

Was die grafisch ermittelten 5.42 bestätigt.

Answer 3

Die Kurve sieht schon ganz gut aus.
Den Wert bei y = 5 halte ich eh für einen Ausreißer.

~plot~ { 2.796| 20 } ; {2.724 | 10} ; {2.620 | 5 } ; { 2.171|2.5 } ; {1.417 |1.25 } ; {0.87 | 0.63} ; {0.495 | 0.31} ; [[ 0 | 3 | 0 | 21 ]] ;  ; tan ( 0.542 * x ) * 1.11 ~plot~

Answer 4

Ich gehe mal davon aus das die Messwerte Absorptionseinheiten (ABS, EXT oder CU ) sind.

In der Photometrie sind Absorptionen hoeher als 1,5 nicht mehr brauchbar da dann eine Abweichung vom Lambert Beerschen Gesetz      ABS = Absorptionskoeffizient x OPL x concentration  auftritt.

Also sobald nicht mehr eine Gerade erhalten wird beim auftragen von Absorption vs concentration oder umgekehrt muss man den Messaufbau veraendern .

1. Konzentration zu gross = Messwert zu gross = OPL zu gross

das erreicht man in dem man eine kleiner Kuvette benutzt ( gibt es als 1 mm, 2mm, 5mm, 10mm, 20mm, ...)

Dann neu kalibrieren und schauen das man nahezu eine Gerade bekommt.

Werte ueber 2 sind Fahrkarten und Unsinn!

Glaubs mir ich mache Photometrie seit 30 Jahren..

Gruss

Helmut