Oberflachenberechung einer funktion

Question

Zu lösen gilt folgende Aufgabe:

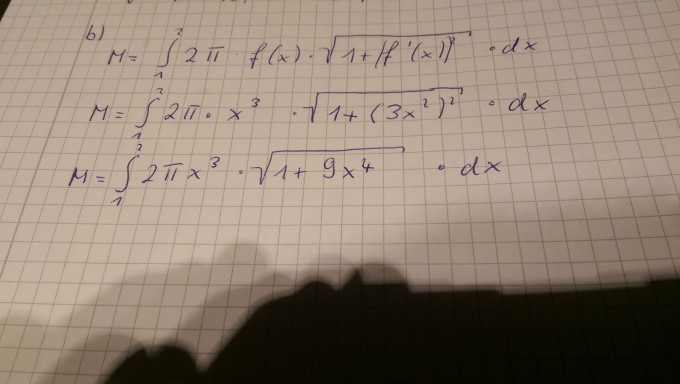
Das ist ja erstmal die Formel, dann wollte ich das partiell integrieren.

Dann habe ich gesagt f'=2pix^3 und g= gleich das andere.

Dann steht ja dort:

f * g - integral aus: f * g'

Dann steht ja beim integral: pi/2 X^4 * 18x^3/sqrt(1+9x^4) *dx

Dann wollte ich substituieren: u=x^4

Dann steht dort ja: pi/2*u / sqrt(1+9u) *du und vordem integral steht dann 1/2

Wie mache ich jetzt weiter?

Bitte um Hilfe

Comments

Substituiere direkt von Anfang an und schmeiß die partielle Integration über Board.

---

Ok, und wonach soll ich dann von Anfang an substituieren dann auch wieder u=x^4?

---

Ne das macht ja dann keinen sinn

---

Ja. Damit kriegst du auch das lästige \(x^3\) dann "weg".

Answer 1

Substitution z = 1+9x⁴   →  dz/dx = 36 x³  →  dx = dz / (36 x³)

∫ ...   = 2π • ∫_z1^z2   x³ • √z • dz/(36x³)  dz =  π/18 ∫_z1^z2  √z dz  = π/18 • 2/3 [z^3/2]_z1^z2 

=  π/27• [ (1+9x⁴)^3/2 ]₁² ≈ 199,48

Gruß Wolfgang