Hallo Nikola,
1. Falls a genau 1 oder -1 ist, ist die Parabel weder gestreckt noch gestaucht.
2. Wenn a positiv ist, ist die Parabel nach oben geöffnet, ansonsten (bei negativem a) nach unten.
3. Ist der Betrag von a größer als 1 (z.B. bei a= -5 oder a= +5), verläuft die Parabel enger/ schmaler als eine Parabel mit a=±1. Die Parabel gilt dann als (in y-Richtung) gestreckt.
4. Ist der Betrag von a kleiner als 1 (z.B. bei a= -0,8 oder a= +0,8) ist die Parabel breiter als eine Parabel mit a=±1. Die Parabel gilt dann als (in y-Richtung) gestaucht.
5. Ist a Null, gilt y = 0x²+bx+c = bx+c. Das ist dann gar keine Parabel mehr sondern eine Gerade (mit Steigung b und y-Achsenabschnitt c). Das bedeutet dass a bei einer Funktion in der Form y = ax²+bx+c nicht Null sein darf wenn es eine Parabel sein soll.
6. Bei x handelt es sich um die Zahl, die in die Funktion eingesetzt wird, um einen (zu dem x) zugehörigen y-Wert zu berechnen. Ein Punkt auf dem Graphen ergibt sich aus dem x- und dem zugehörigen y-Wert. Zu jedem x-Wert gibt es maximal einen y-Wert.
Beispiel: Die Funktion sei z.B. y=3x²-4x+5 (d.h. a=+3, b=-4, c=+5).
Nun wird der Funktionswert (y-Wert) z.B. für x= -0,5 gesucht.
Durch Einsetzen von -0,5 für x ergibt sich
y(-0,5)= 3(-0,5)²-4(-0,5)+5= 0,75+2+5= 7,75, d.h. der Punkt mit x=-0,5 und y=7,75 befindet sich auf dieser Parabel.
Für x= 1 ergibt sich y(1)= 3(1)²-4(1)+5= 4, d.h. der Punkt mit x=1 und y=4 befindet sich auch auf der Parabel.
Auf diese Art und Weise lassen sich durch Einsetzen zu beliebigen x-Werten zugehörige y-Werte (und damit Punkte auf der Parabel) bestimmen.
Man kann auch prüfen ob ein bestimmter gegebener Punkt auf der Parabel liegt, z.B. (x=2/ y=8):
y(2)= 3(2)²-4(2)+5= 12-8+5= 9, d.h. der Punkt (2/8) liegt nicht auf der Parabel, dafür der Punkt (2/9).
7. c gibt den y-Wert an, an dem die Parabel die y-Achse schneidet. Für diesen Schnittpunkt mit der y-Achse gilt x=0, denn x=0 ist die Stelle, durch die die y-Achse von unten nach oben durch den Koordinatenursprung (x=0/y=0) verläuft.
Bei dem Beispiel oben (y=3x²-4x+5) ist der y-Achsenabschnitt damit 5 und der Punkt mit x=0 und y=5 liegt auf der Parabel.
8. b ist der am Schwierigsten zu verstehende Parameter.
Mit b und a gemeinsam kann z.B. die x-Koordinate des Scheitelpunkts der Parabel berechnet werden. Der Scheitelpunkt ist bei einer nach oben geöffneten Parabel der "tiefste" Punkt (d.h. derjenige Punkt mit dem kleinsten y-Wert welcher auf der Parabel liegt) oder bei einer nach unten geöffneten Parabel der "höchste" Punkt (d.h. derjenige Punkt mit dem größten y-Wert welcher auf der Parabel liegt).
Die x-Koordinate des Scheitelpunktes einer Parabel in der Form y= ax²+bx+c kann allgemein wie folgt berechnet werden:$${ x }_{ S }=\frac { -b }{ 2a } $$
In dem Beispiel oben hatten wir y=3x²-4x+5, d.h. a=+3 und b=-4.
Die x-Koordinate des Scheitelpunkts ist damit in dem Beispiel
$${ x }_{ S }=\frac { -(-4) }{ 2\cdot 3 } =\frac { 2 }{ 3 } \approx \quad 0,667$$
Durch Einsetzen kann die zugehörige y-Koordinate bestimmt werden:
$${ y }_{ S }=\quad 3\cdot { \left( \frac { 2 }{ 3 } \right) }^{ 2 }-4\cdot \frac { 2 }{ 3 } +5=\quad 3\cdot \frac { 4 }{ 9 } -4\cdot \frac { 2 }{ 3 } +5=\quad \frac { 4 }{ 3 } -\frac { 8 }{ 3 } +\frac { 15 }{ 3 } =\quad \frac { 11 }{ 3 } \approx \quad 3,667$$
D.h. der Scheitelpunkt hat in diesem Beispiel die Koordinaten x=2/3 und y=11/3 und es gibt auf dieser (wegen a>0 nach oben geöffneten und wegen |a| > 1 gestreckten) Parabel keinen Punkt mit kleinerer y-Koordinate als 11/3.
Graph der Funktion y=3x²-4x+5 (Beispiel):
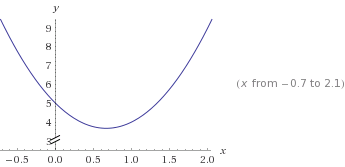
9. Spezialfall Normalparabel:
a=1, b=0, c=0 => y=x²: Verläuft durch den Koordinatenursprung (0/0) wegen c=0. Scheitelpunkt ebenfalls (0/0). Weder "gestaucht" noch "gestreckt" wegen a=1. Nach oben geöffnet wegen a > 0.
Zum Abschluss noch ein anderes vollständiges Beispiel zum Verständnis:
y= -0.6x²-2x-3
→ a = -0,6
→ b = -2
→ c = -3
(1) Die Parabel ist gestaucht wegen |a| = |-0,6| = 0,6 < 1
(2) Die Parabel ist nach unten geöffnet wegen a < 0
(3) Die Parabel schneidet die y-Achse im Punkt (0/-3) wegen c= -3
(4) Die x-Koordinate des Scheitelpunkts ist -b/2a = -(-2) / 2*(-0,6) = -5/3 (≈ -1,667)
(5) Die y-Koordinate des Scheitelpunkts ist y(-5/3) = -0,6*(-5/3)²-2*(-5/3)-3= -4/3 (≈ -1,333)
(6) Graph der Funktion y= -0.6x²-2x-3 (Beispiel 2):
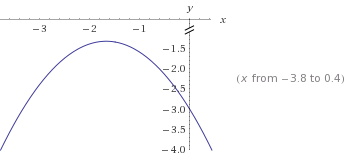
LG!