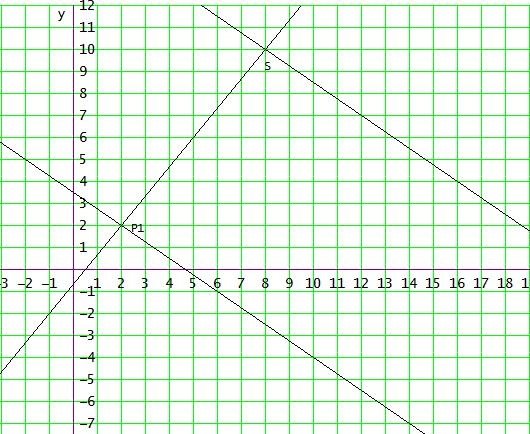
P1(2|2) liegt auf dem Graph von f1
Senkrechte zum Graph von f1 durch (2|2) hat die Steigung -1/(-3/4) = 4/3 :
y = 4/3 • (x -2) + 2 = 4/3 x - 2/3
Wenn du diese mit f2 schneidest findest du den Schnittpunkt S(8|10)
4/3 x - 2/3 = -3/4 x +16 → x = 8 → y = 10
Der Abstand P1S ist der gesuchte Abstand der beiden Geraden:
√((8 - 2)2 + (10 - 2)2) = 10
Gruß Wolfgang