Parabel schneidet x Achse auf gegebenen Punkten - Zeichnen

Question

ich bräuchte Hilfe bei einer Aufgabe, sie lautet:

Eine Normalparabel schneidet die x-Achse an den Punkten P(-2|0) und Q(6|0)

Ich würde gerne wissen, wie man die Scheitelform bzw. die Funktionsgleichung errechnen kann

Answer 1

Eine Normalparabel schneidet die x-Achse an den Punkten P(-2|0) und Q(6|0)

Die kürzeste Variante basiert auf der Überlegung das der Scheitelpunkt sich
in der Mitte der beiden Nullstellen befindet

x = ( -2 + 6 ) / 2 = 2
Scheitelpunktform
f ( x ) = ( x - 2 )^2 + b
Einsetzen
f ( 6 ) = ( 6 - 2 )^2 + b  = 0
16 + b = 0
b = -16

Answer 2

Eine Normalparabel schneidet die x-Achse an den Punkten P(-2|0) und Q(6|0)

Ansatz aufgrund der Nullstellen. 
y = (x+2)(x-6) 

nun noch die Klammern auflösen und daraus dann die Scheitelpunktform basteln. 
~plot~(x+2)(x-6) ; [[10]]~plot~Wenn nötig: Schau mal dieses Video an:

Answer 3

das Verfahren ist nicht das kürzeste, funktioniert aber mit zwei beliebigen gegebenen Punkten, auch wenn es sich nicht um Nullstellen handelt:

Scheitelform :  f(x) =( x - a )² + b

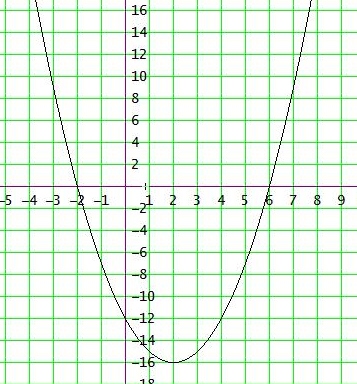
Die Parabel verläut durch die Punkte (-2|0) und (6|0)

f(-2) = (-2-a)² + b = 4 + 4a + a² + b = 0 → b =  -4 - 4a - a²

f(6) = (6-a)² + b = 36 - 12a + a² + b = 0

36 - 12a + a²    - 4 - 4a - a² = 0

32 - 16a  = 0

32 = 16a

a = 2   →  b = -16

Scheitelform:  f(x) = ( x - 2 )² - 16

Gruß Wolfgang