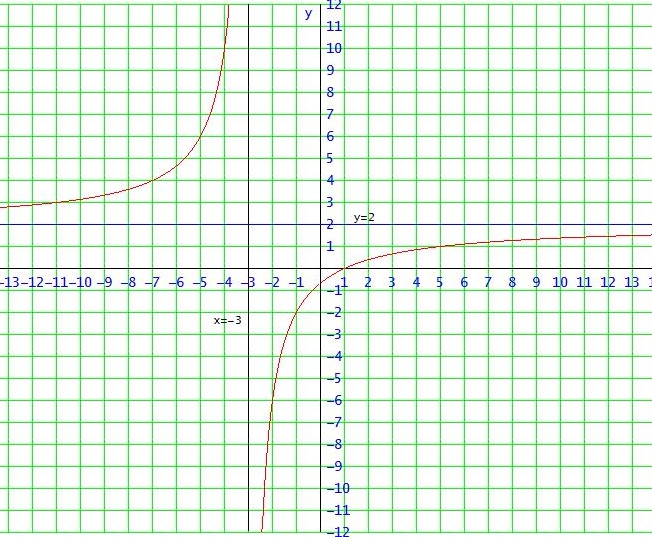
f(x) = 2 • (x2 - x) / (x2 + 3x) = 2 • x • (x-1) / [ x • (x+3) ] =D 2 • (x-1) / (x+3) [ → 2 für x→ ±∞ ]
Nullstelle: x=1 , Polstelle: x= -3 , x=0 ist stetig behebbare Lücke (im Bild nicht erkennbar!)
die Asymptoten sind x= -3 (senkrechte Asymptote an der Polstelle)
und y = 2 (Gerade, der sich der Graph für x→∞ annähert)
wenn du zweimal die Quotientenregel [ u/v ] ' = ( u' • v - u • v ' ) / v2 anwendest, erhältst du
f ' (x) = 8 / (x + 3)2
f '' (x) = - 16/(x + 3)3
Gruß Wolfgang