Deine Frage ist berechtigt, weil es für die Binomialverteilung 4 unterschiedliche Fälle gibt:
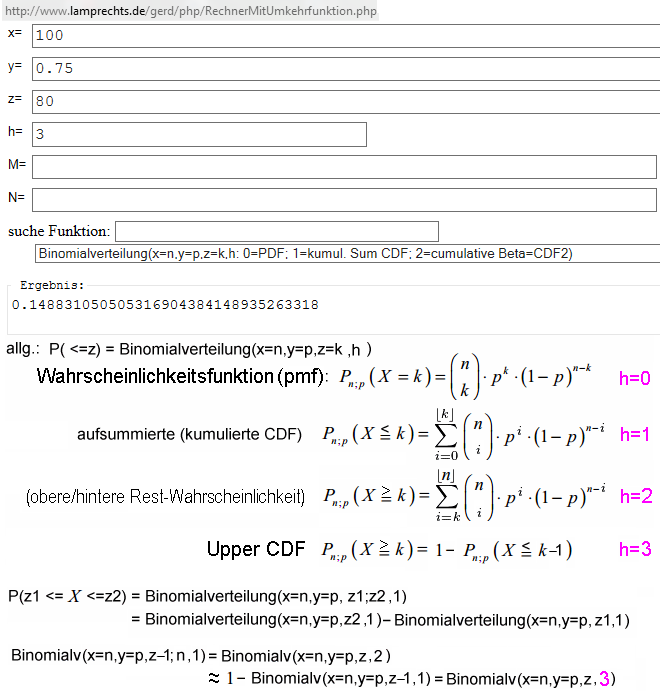
http://www.lamprechts.de/gerd/php/RechnerMitUmkehrfunktion.php
unterscheidet diese mit dem letzten Parameter h.
Dein Fall F(...) entspricht die untere aufsummierte Wahrscheinlichkeit (CDF) P(X ≤k) also h=1.
Gesucht ist aber die obere (Upper) CDF: P(X≥k)
Da die die meisten Rechner h> 1 nicht kennen, gibt es 2 Wege:
h=2 : selbst Summe bilden, so wie Der_Mathecoach
h=3: 1- P(X ≤ k-1) das ist der "Rest", da Gesamtwahrscheinlichkeit immer 1 ist.
Interessant: wenn man auf über 32 Stellen nachrechnet, gibt es Unterschiede ab der 10. Stelle:
Binomialv(100,0.75,80,2)=0.1488310504429912583746969814346544
Binomialv(100,0.75,80,3)=0.148831050505316904384148935263318
zu c)
kommt man auch mit Probieren hin, da die Umstellung nicht ganz einfach:
Binomialv(100,0.75,82,3)=0.063011417324915846927653901868147
Binomialv(100,0.75,83,3)=0.037626263763510240933775534565376
Hinweis: 90% aller Rechner (und ich hier) benutzen zur Dezimalzeichentrennung den Punkt .
(da Komma zum Trennen von Parametern reserviert ist)
Wenn man beim Umkehrfunktionen Rechner für Parameter z 2 Werte mit ; getrennt eingibt, hat man gleich die Differenz.