Untersuchen Sie die folgenden Funktionen (stetige Ergänzung) a) f(x) = x^2 / tan x, b) g(x) = (x^2 - πx)/ sinx

Question

Untersuchen Sie für die folgenden Funktionen, welche Lücken sich Definitionsbereich ergeben, wenn man alle reellen Zahlen zu Grunde legt, und stellen Sie fest, welche dieser Lücken sich durch stetige Ergänzung beheben lassen.

a) \( f ( x ) = \frac { x ^ { 2 } } { \tan x } \)

b) \( g ( x ) = \frac { x ^ { 2 } - \pi x } { \sin x } \)

Comments

Überleg mal, wann ist ein Bruch nur definiert bzw. wann kann man einen Bruch ausrechnen?

Wenn du den Bruch nicht ausrechnen kannst, dann hat die Funktion an dieser Stelle keinen Wert.

Ansonsten schau dir mal das an:

Ansonsten plotte doch mal die Funktionen

---

Ach ja überleg dir einfach, an den Stellen wo die Funktion nicht definiert ist, welchen Wert hätte sie, wenn sie definiert wäre (z.B. über ein plotter)

:)

Viel Spaß noch

Answer 1

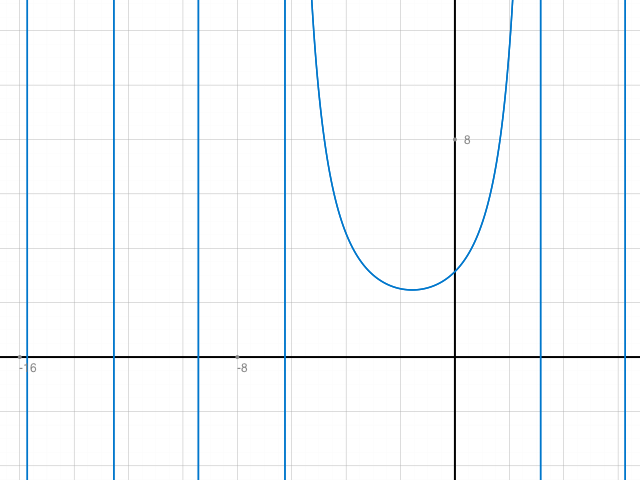
a) f(x) = x² / tan x

Definitionslücken bei kπ/2 , k Element Z.

k ungerade unmöglich, weil dann tan x gar nicht definiert ist. k gerade nicht möglich, weil da tan x =0 und Division durch 0 nicht definiert ist.

Gemäss Skizze im Bereich (-3,3) sind die Definitionslücken stetig hebbar. Also konkret bei 0, -π/2 und π/2. Ausserdem (vgl. Kommentar) sind alle Unstetigkeiten in kπ/2 , mit k ungerade stetig hebbar mit f(kπ/2) :=0.

Nicht hebbar sind nur die Unstetigkeitsstellen in kπ, k Element Z \ {0}.

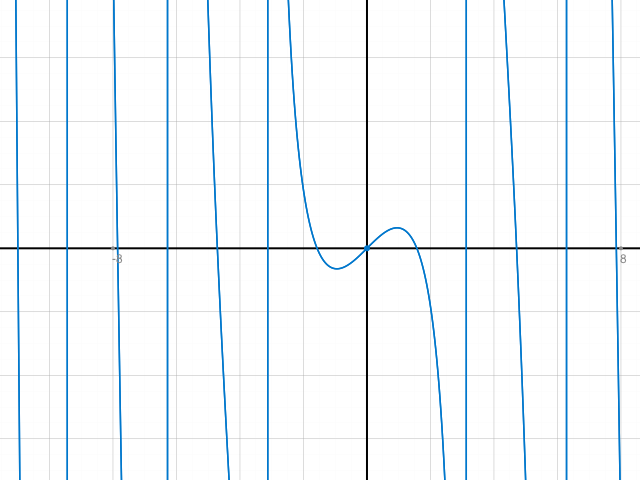
g(x) = (x² - πx)/ sinx

Definitionslücken bei x= kπ, k Element Z.

Gemäss Skizze im Bereich (-6, 2.5). D.h. bei -π und 0 ist die Definitionslücke stetig stopfbar.

 

Comments

Sind die Definitionslücken bei a) so richtig beschrieben? Was ist, wenn  x = 0?

---

ok. Danke. Wurde korrigiert...

0^2/ tan(0) ist offenbar stetig stopfbar mit f(0) = 0.

---

Nochmal zu a): Für ungerade  k  ist  tan(kπ/2)  tatsächlich nicht definiert. Laut Skizze sind aber die Funktionswerte an diesen Stellen gleich Null. Damit ist die Funktion an allen Stellen  x = kπ/2  mit ungeraden  k  vermöge  f(kπ/2) = 0  stetig fortsetzbar und nicht nur für  k ∈ {-1,1}.