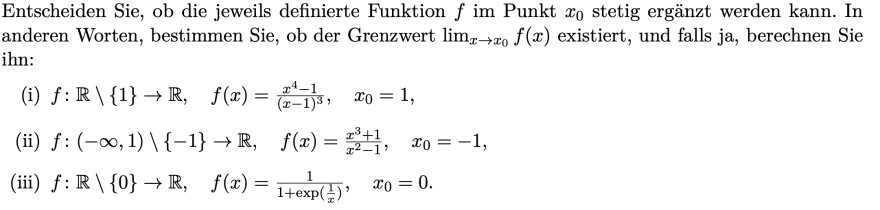
Text erkannt:
Entscheiden Sie, ob die jeweils definierte Funktion \( f \) im Punkt \( x_{0} \) stetig ergänzt werden kann. In anderen Worten, bestimmen Sie, ob der Grenzwert \( \lim \limits_{x \rightarrow x_{0}} f(x) \) existiert, und falls ja, berechnen Sie ihn:
(i) \( f: \mathbb{R} \backslash\{1\} \rightarrow \mathbb{R}, \quad f(x)=\frac{x^{4}-1}{(x-1)^{3}}, \quad x_{0}=1 \),
(ii) \( f:(-\infty, 1) \backslash\{-1\} \rightarrow \mathbb{R}, \quad f(x)=\frac{x^{3}+1}{x^{2}-1}, \quad x_{0}=-1 \),
(iii) \( f: \mathbb{R} \backslash\{0\} \rightarrow \mathbb{R}, \quad f(x)=\frac{1}{1+\exp \left(\frac{1}{x}\right)}, \quad x_{0}=0 \).
Aufgabe: