Hoch-, Tief und Sattelpunkt: f(x)= x³ - 6x²+2

Question

Untersuche sie funktion f auf Hoch Tief und Sattelpunkte

f(x)= x³ - 6x²+2

f(x)= x³ - 75x

Answer 1

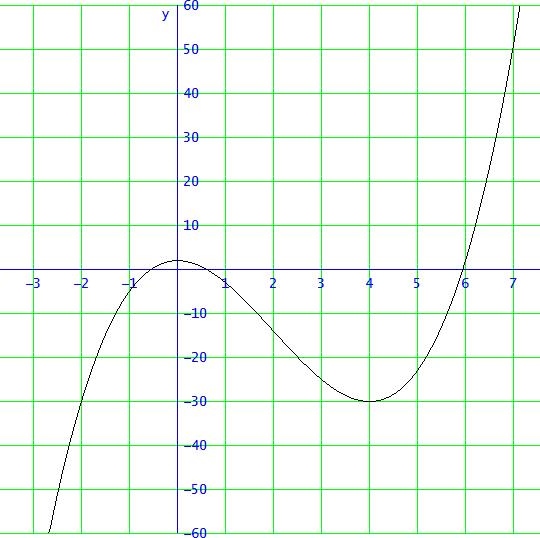
f(x)= x³ - 6x² + 2

f '(x) = 3·x² - 12·x = 0  ⇔ x = 0 oder x = 4

f ''(x) = 6x -12  

f ''(0) = -12 < 0  und f(0) = 2  → H(0|2)

f ''(0) = 12 > 0  und f(4) = -30  → T(4|-30)

f "(x) =  6x -12 = 0  ⇔  x  = 2

f '''(2)  ≠ 0 und f(2) = -14   →  W(2|-14), kein Sattelpunkt (f '(2)≠0)

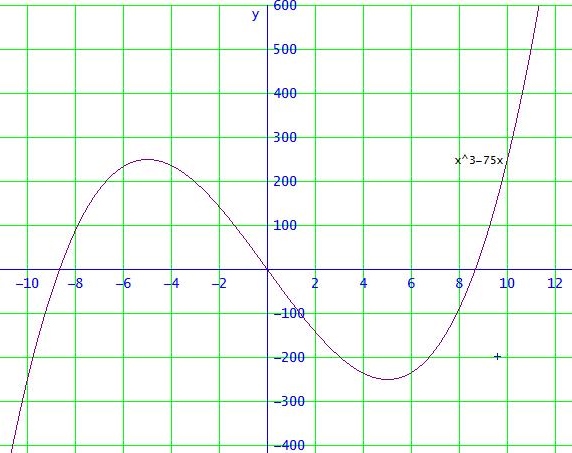
f(x)= x³ - 75x    analog. 

Hier kannst du die Lösungen (ungefähr) vergleichen:

Gruß Wolfgang

Answer 2

hier ein nützlicher Link dazu:

http://matheguru.com/rechner/kurvendiskussion/