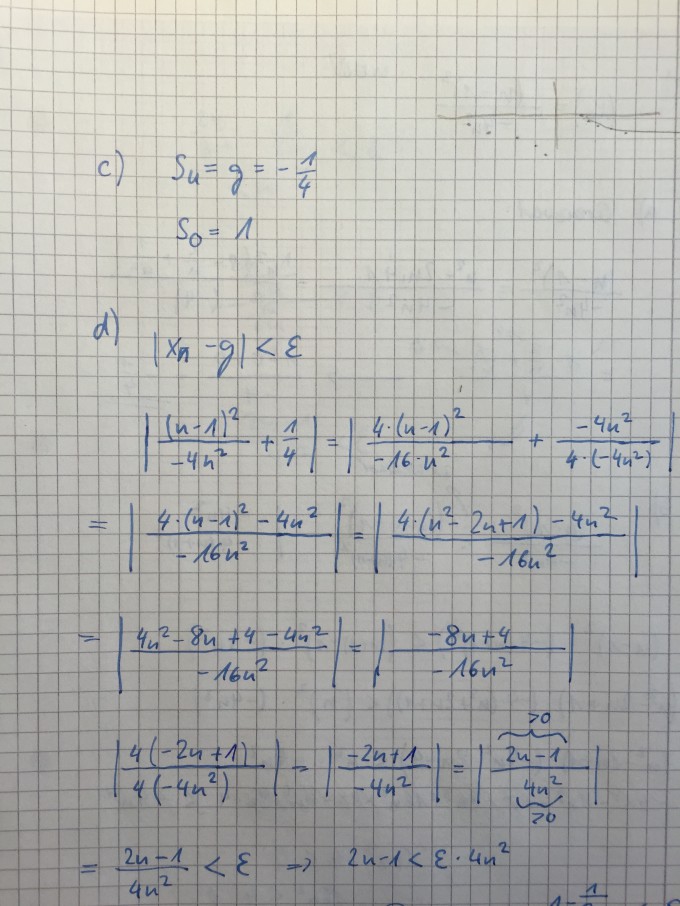Es geht um die Aufgabe 8 d)
Wie rechne ich am Ende weiter? Ich muss ja nach n auflösen, doch wie mache ich das?
Obere Schranke = 0 (nicht 1)
danke im voraus
Aufgabe
8). Gegeben sei die Folge \( \left(x_{n}\right)=\frac{(n-1)^{2}}{-4 n^{2}} \) für \( n \in \mathbb{N} \)
a) Berechnen Sie den Grenzwert \( \mathrm{g} \in \mathbb{R} \) der Folge \( \left(\mathrm{x}_{\mathrm{n}}\right) \)
b) Untersuchen Sie die Folge \( \left(x_{n}\right) \) auf strenge Monotonie (mit Nachweis!).
c) Zeigen Sie, dass die Folge \( \left(\mathrm{x}_{\mathrm{n}}\right) \) beschränkt ist und geben Sie Schranken an.
d) Bestimmen Sie \( \mathrm{N}(\varepsilon) \in \mathbb{N} \) für \( \varepsilon>0, \) so dass \( \left|\mathrm{x}_{\mathrm{n}}-\mathrm{g}\right|<\varepsilon \) für alle \( \mathrm{n} \geq \mathrm{N}(\varepsilon) \) gilt
wobei g der Grenzwert der Folge \( \left(x_{n}\right) \) sei; d. h. es gilt \( \lim \limits_{n \rightarrow \infty} x_{n}=g . \)
Bitte geben Sie beim Auflösen des Betrages eine Begründung an.
e) Bestimmen Sie mithilfe von Aufgabenteil d) den Index \( N(\varepsilon) \in \mathbb{N} \) für \( \varepsilon=10^{-2} \)
Hinweis: Verwenden Sie für 8 ). c) und \( d \) ) Ihre Ergebnisse aus 8 ). a) bzw. b).