Hallo miteinander,
ich habe die Ungleichung:
$$ \frac { x+2 }{ 2x-5 } -1\le 0 $$
So ich habe jetzt zwei Fälle unterschieden:
Fall 1:
2x-5>0
x>2,5
und
$$ \frac { x+2 }{ 2x-5 } -1\le 0 $$
x >= 7
Fall 2:
2x-5<0
x<2,5
$$ \frac { x+2 }{ 2x-5 } -1\le 0 $$
x >= 7
Georgborn sagt an dieser Stelle, dass man sich Lösungen oft mit dem Zahlenstrahl verdeutlichen soll. Daher habe ich das ganze mal gezeichnet.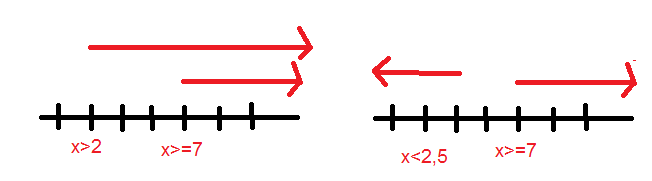
So:
x>2 und x>=7 macht für mich Sinn. x<2,5 und x>= macht für mich keinen Sinn. Aber woher erkenne ich jetzt die Lösungsmenge?