Hi,

Satz 6.7.15 (a):
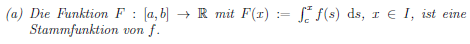
Soweit ich weiß bedeutet
$$\triangledown G(x,u,v)=\left( G(x,u,v)\frac { d }{ dx } ,G(x,u,v)\frac { d }{ du } ,G(x,u,v)\frac { d }{ dv } \right) ^{ }$$
und es gilt
$$ G(x,u,v)\frac { d }{ dx } ={ \frac { 1 }{ x } { e }^{ xy }| }_{ y=u }^{ y=v } $$
(Ableitung nach x ins Integral gezogen und dann nach y Integriert)
Aber
$$ G(x,u,v)\frac { d }{ du } =-\frac { { e }^{ xu }+{ e }^{ u } }{ u } \frac { d }{ du } $$
oder?
Nach Satz Satz 6.7.15 (a) gilt doch:
$$ G(x,u,v)\frac { d }{ du } =\left( \int _{ u }^{ v }{ \frac { { e }^{ xy }+{ e }^{ y } }{ y } dy } \right) \frac { d }{ du } =\left( -\int _{ v }^{ u }{ \frac { { e }^{ xy }+{ e }^{ y } }{ y } dy } \right) \frac { d }{ du } =-\frac { { e }^{ xu }+{ e }^{ u } }{ u } \frac { d }{ du } $$
Wo liegt mein Denkfehler?