a) Dein Ansatz
(1) f(xp) = g(xp)
(2) f'(xp) * g'(xp) = -1
ist auf jeden Fall richtig.
Allerdings hast du die eine Ableitung falsch berechnet:
f(x) hast du richtig abgeleitet:
f(x) = ax2
f'(x) = 2ax
g(x) = 1/2 * (1/x2)
g'(x) = - 1/x3
Jetzt stellst du das Gleichungssystem auf:
(1) ax2 = 1/2*(1/x2)
(2) 2ax*(-1/x3) = -1
=>
(1*) x4 = 1/(2a)
(2*) 1/x2 = 1/(2a)
Setzt beide gleich, um die Stelle zu erhalten:
x4 = 1/x2
x6 = 1
x = ±1
Einsetzen in (1*):
1 = 1/(2a)
2a = 1
a = 1/2
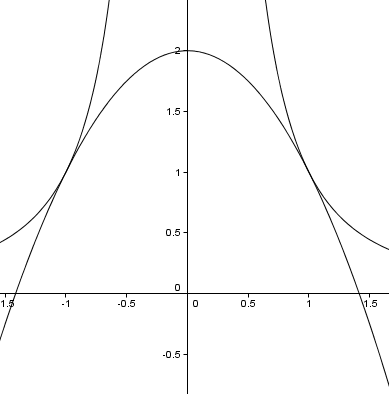
Für a = 1/2 schneiden sich die beiden Funktionen also an den Stellen x=1 und x=-1 im rechten Winkel.
b) Hier funktioniert so ähnlich, dein Ansatz ist wieder richtig.
f(x) = -x2+c
f'(x) = -2x
g(x) = 1/(x2)
g'(x) = -2/(x3)
(1) -x2+c = 1/(x2) |*(-x2)
(2) -2x = -2/(x3) |*(-x3/2)
(1*) x4-cx2 + 1 = 0
(2*) x4 = 1
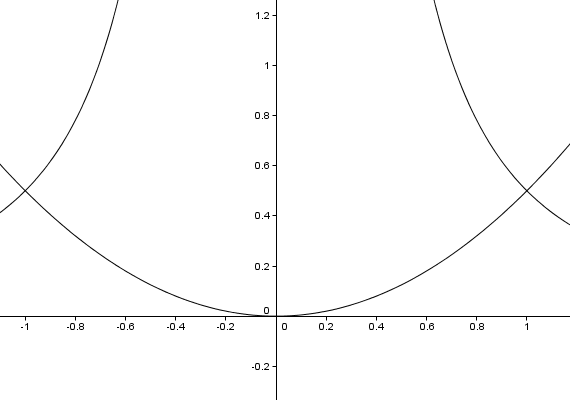
Aus (2*) folgt wieder x = ±1.
Eingesetzt in (1*):
1 - c + 1 = 0
2 - c = 0
c = 2
Auch hierzu noch ein Bild: