f(x) = x3*(7-x)1/2 Berechnen Sie Nullstelle, Minimum und Maximum und Integral von x3*(7-x)3*dx

Question

Aufgabe:

Es sei

$f:[-2,7] \rightarrow \mathbb{R}, \quad x \mapsto x^{3} \sqrt{7-x}$

i) Bestimmen Sie die Nullstellen, das Minimum und das Maximum von $f$. Zeichnen Sie den Graphen von $f$. Hinweis: $f^{\prime \prime}$ und höhere Ableitungen müssen nicht berechnet werden.

ii) Berechnen Sie

$\int \limits_{0}^{7} x^{3} \sqrt{7-x} d x$

mittels der Substitution $7-x=t^{2}$.

Answer 1

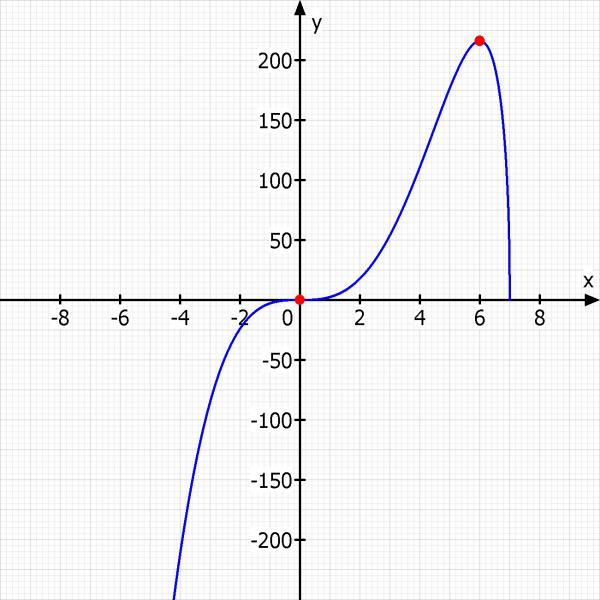
f(x) = x³·√(7 - x) D = ]-∞; 7]

f'(x) = x²·(42 - 7·x)/(2·√(7 - x))

Nullstellen f(x) = 0

Die kann man ablesen. Einmal bei 0, dann ist 0³ = 0 und einmal bei 7, dann ist √(7 - 7) = 0

Extremstellen f'(x) = 0

Auch diese sind ablesbar bei 0, dann ist x² = 0 und 6, dann ist (42 - 7·6) = 0

f(0) = 0 
f(6) = 6³·√(7 - 6) = 216

Kleine Skizze:

Comments

Eine Stammfunktion findest Du wie folgt

https://www.wolframalpha.com/input/?i=integral+x%5E3*%E2%88%9A%287-x…

Für das bestimmte Integral sollte man auf einen wert von 10976·√7/45 = 645.3 kommen.