Flugbahn Geraden Aufgabe

Question

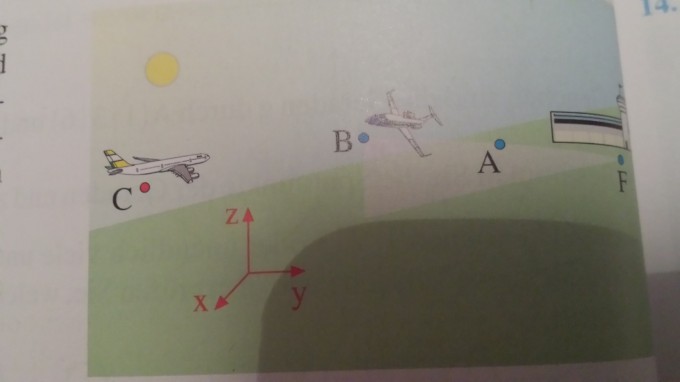
Flugzeug Alpha fliegt geradlinig durch  die Punkt  A (-8/3/2) und B (-4/-1/4). Eine Einheit im Koordinatensystem entspricht einem Kilometer.  Der Flughafen F befindet sich in der x-y Ebene.

a) in welchem  Punkt F ist das Flugzeug gestartet? In welchem Punkt  T erreicht es seine Reiseflughöhe von 10000m?

g: -8/3/2  + r*(4/-4/2)

Punkt F:

z=0

F (-12/7/0)

Punkt T:

z=10000

T (19988/-19993/10000) ???

b)

Flugzeug BETHA steuert Punkt C (10/-10/5) aus Richtung v= (-2/2/-1) an. Zeigen die dass die beiden Flugzeuge keinesfalls kollidieren können.

Richtungsvektoren  sind parallel -2 * (-2/2/-1) = 4/-4/2

Ich wollte die Gleichungen gleichsetzen bzw. Gleichungssysteme aufstellen aber irgendwie erhalte ich keine Zahl für ein Parameter,  da wenn ich z.b. Parameter r eliminiere, eliminiert sich auch s.

I. 10 - 25 = -8 + 4r

II. -10 + 2s = 3-4r

III. 5 - s = 2 + 2r

c) in dem Moment an dem Flugzeug alpha den Punkt  B passiert, erreicht Flugzeug beta den Punkt  C. Wie groß  ist die Entfernung der Flugzeuge zu diesem Zeitpunkt?

BC: (10--4 / -10-1/ 5-4) = (14/-9/1)

IBCI = 16,67 m

d) Beim Passieren von Punkt C wird Flugzeug Beta vom Tower aufgefordert in Richtung  v1: (-5/4-1) weiterzufliegen. On 1000m Höhe soll eine weitere Kursanderung erfolgen, die die Flugzeug BETA zum Flughafen F bringt. In welche Richtung  muss diese letzte korektur  das flugzeug fuhren?

Beta beim passieren C : 10/-10/5 + s* (-5/4/-1)

z= 1000

1000= 5-s

995= s

??

Dankeschön 

Comments

EDIT: Nur mal zu deiner Geradengleichung (?)

g: -8/3/2  + r*(4/-4/2)  ist keine Gleichung, da kein Gleichheitszeichen vorkommt. Links fehlt dann der allgemeine Ortsvektor ( r^Pfeil = (x|y|z) ) der Geraden mit dem Namen g. Auch fehlen Klammern um den Stützvektor .

Du meinst hier 

g:  r^Pfeil =  (-8/3/2)   + t*(4/-4/2)        

Answer 1

Hallo samira,

Zu a):

Der Punkt F(-12/7/0) ist richtig. Der Punkt T ist leider falsch.

Aufgabentext: "Eine Einheit im Koordinatensystem entspricht einem Kilometer"

D.h.: T(x/y/10), denn 10000 m Flughöhe = 10 km.

Vektor AB = (4/-4/2)
g_AB: Vektor x = (-8/3/2) + z * (-4/4/2), z ∈ R

Mit T erhält man:

(x/y/10) = (-8/3/2) + z * (-4/4/2)

3. Zeile nach z auflösen:
10 = 2 + 2z
4 = z

z = 4 in g eingesetzt: T(8/-13/10)

Zu b): Die Richtungsvektoren sind Vielfache voneinander, d.h. g (Flugzeug Alpha) und h (Flugzeug Betha) sind parallel. Daraus folgt: Es gibt keinen Schnittpunkt, die beiden Flugzeuge können keinesfalls kollidieren.

Zu c): Falsche Einheit, es sind 16.67 km. :-)

Zu d): Die Geradengleichung hast du richtig aufgestellt:

g_C: Vektor x = (10/-10/5) + z * (-5/4/-1)

Aufgabentext: "In 1000m Höhe soll eine weitere Kursänderung erfolgen"

Damit hast du die z-Koordinate gegeben (1000 m = 1 km), betrachte daher:

1 = 5 - z
4 = z

=> P(-10/6/1)

Stelle mit dem Punkt P eine Geradengleichung auf. Diese Gerade geht durch den Punkt F (bereits bei a) berechnet), siehe Aufgabentext. Stelle die Geradengleichung g auf:

g: Vektor x = Vektor OP + z * Vektor PF
g: Vektor x = (-10/6/1) + z * (-12 - (-10) / 7 - 6 / 0 - 1)

g: Vektor x =  (-10/6/1) + z * (-2/1/1)

Damit hast du den Richtungsvektor (-2/1/1) als Lösung für den Aufgabenteil d).

Comments

Der Richtungsvektor bei der d) ist (-2/1/-1) ;)

---

Wie komme ich eigentlich auf den Punkt F?