Extrema einer ln-Funktion

Question

F(x)=ln(10^-5 +cos^2x) 

Es sollen die Extrema der Funktion bestimmt werden. Ich habe die erste Ableitung berechnet aber über die Ableitung hinaus weiß ich leider nicht weiter. 

Kann mir jemand beim Umstellen helfen, über Ansätze wäre ich sehr dankbar !!!

Comments

heißt es
[ cos  ( x ) ]^2
gleichwertig zu
cos^2 ( x )

---

Entschuldigung da habe ich mich vertippt, es soll richtig heißen: 
f(x)=ln (10^-5 +cos^2 (x)) 

Answer 1

f(x) = LN(COS(x)^2 + 1/100000)

überlege dir warum es langt die Extrema von

f2(x) = COS(x)^2 + 1/100000

überlege dir warum es langt die Extrema von

f3(x) = COS(x)^2

Vermutlich kannst du mir jetzt bereits die Extrema aus dem Kopf sagen.

Answer 2

Funktion
1.Ableitung
[ ln ( term )  ] ´ = 1 / ln ( term ) *  ( term ´ )
Extrema 1.Ableitung = 0
Ein Bruch ist dann null wenn der Zähler 0 ist

~plot~ ln ( 10^5 + (cos(x))^2 )  ;   [[ 0| 4 | 11.512925 | 11.512936 ]] ~plot~

Comments

Danke für deine Antwort, also ich habe die Ableitung berechnet und bin zu dem Ergebnis gekommen, dass die Nullstellen bei kpi/2 liegen müssten. Nun weiß ich aber nicht recht wie ich dann zu den Nullstellen komme, 

Weil bei normalen Funktionen hab ich es dann immer in die 2 Ableitung gesetzt und bestimmt ob max oder Minimum. In diesem Fall  weiß ich nicht weiter ..

---

Meine Antwort enthält einen Fehler bei 10^{-5}, Da habe ich
10^5 eingesetzt.

Die Aufgabe ist folgendermassen aufgebaut.
(cos(x))^2 ist Null oder positiv
(cos(x))^2 + 1/10^5 ist stets posiiv
Der ln ( ) ist damit immer gegeben.
D = ℝ

Hier meine Berechnungen

 

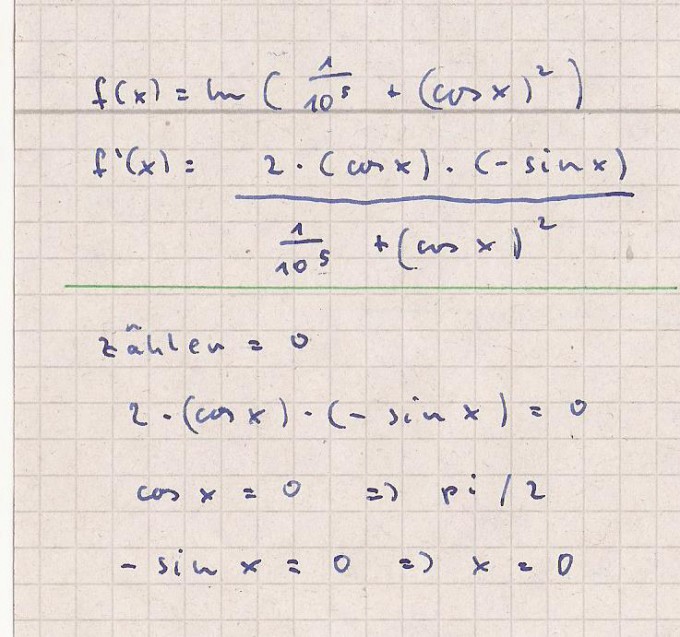
Extremstellung 1.Ableitung = 0
Ein Bruch ist dann 0 wenn der Zähler 0 ist.

2 * ( cos x ) * ( - sin x ) = 0
Satz vom Nullprodukt
Ein Produkt ist dann 0 wenn mindestens 1 der Faktoren null ist.

Es ergeben sich als erste Stellen
x = 0 und x = pi/2

~plot~ ln ( 1/10^5 + (cos(x))^2 ) ; [[ -5 | 5 | -12 | 0 ]] ~plot~

Nachträge

Man kann auch
- 2 * ( cos x ) * ( sin x ) = 0
schreiben.

Wie du siehst wiederholen sich die Extremstellen.
Dies wäre auch in einer Antwort zu berücksichtigen.

Der Funktionswert sollte auch berechnet werden.

Es wird nur nach den Extremstellen gefragt.
Ob es ein Hoch- oder Tiefpunkt ist wird nicht unbedingt erfragt.

mfg Georg

---

Bei der 2.Ableitung kommt ein Lindwurm heraus.

Sonst könnte man die Art des Extrempunkt über die Monotonie ermitteln.

f ´( x ) > 0 = steigend
f ´( x ) < 0 = fallend

In der 1.Ableitung ist der Nenner immer positiv.
also brauchen wir uns nur den Zähler anschauen

lim x −> 0(-)  [ - 2 * ( cos x ) * ( sin x ) ] = -2 * ( positiv ) * ( negativ ) =  positiv
lim x −> 0(+)  [ - 2 * ( cos x ) * ( sin x ) ] = -2 * ( positiv ) * ( positiv ) =  negativ

Die Monotonie wechselt bei x = 0 von steigend auf fallend. Der Punkt ist ein Hochpunkt.

---

Ich möchte mich nochmal für die ausführliche Antwort bedanken!! Ein super Forum ist das hier !

---

Schön zu hören.
Falls du andere / weitere Fragen hast dann wieder einstellen.