Funktion 3.Grades bei -1 eine Nullstelle und bei -2 einen Wendepunkt mit der Wendetangente t mit t: 3x-y+2,5= 0 besitzt.

Question

Der Auftrag ist es, eine "steckbriefaufgabe" draus zu machen. Formel aufstellen + genau erklärenwas gemacht wurde . Ich kann nichts mit den Infos anfangen,  hilfe gesucht! Hier das gegebene: Eine Funktion 3.Grades deren graph bei -1 eine Nullstelle und bei -2 einen Wendepunkt mit der wendetangente t mit t: 3x-y+2,5= 0 besitzt. Ich habe bereits die 3 Ableitungen der Formel : axhoch3+bxhoch2+cx+d Gemacht und f(-1) in die Formel eingesetzt. Außerdem habe ich t(-2) in die 2. Ableitung tangentenformel eingesetzt. Und nun? Bin für jede Antwort dankbar!

Answer 1

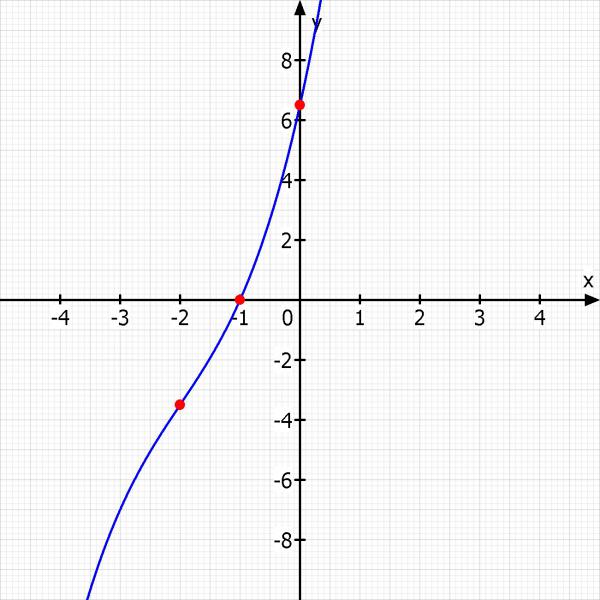
Eine Funktion 3.Grades

f(x) = ax^3 + bx^2 + cx + d

deren graph bei -1 eine Nullstelle

f(-1) = 0

und bei -2 einen Wendepunkt

f''(-2) = 0

mit der wendetangente t mit t: 3x-y+2,5= 0 besitzt.

y = 3x + 2.5 --> Steigung 3
f(-2) = -3.5
f'(-2) = 3

Wir erhalten das Gleichungssystem

-a + b - c + d = 0
-12·a + 2·b = 0
-8·a + 4·b - 2·c + d = -7/2
12·a - 4·b + c = 3

Wir erhalten die Lösung 

a = 0.5, b = 3, c = 9, d = 6.5

Und damit die Funktion

f(x) = 0,5·x^3 + 3·x^2 + 9·x + 6,5

Skizze:

Comments

Vielen lieben dank!!!! Aber ich verstehe nicht , wie sie auf f(-2)-3,5 & f'(-2)=3 gekommen sind (bin nicht sehr helle was das angeht, bin eher der englisch-Spezialist) und was Sie nach dem einsetzen von -1 in der 3.Grad Funktion -a +b -c +d Gemacht haben! Bitte um Erläuterung und Verstanendnis, danke!

---

Der Funktionswert des Graphen f an der Stelle -2 (Wendestelle) muss mit dem Funktionswert des Graphen t an der Stelle 2 übereinstimmen. 

t(-2) = 3*-2 + 2.5 = -3.5

Also 

f(-2) = -3,5

Die Steigung des Graphen f an der Wendestelle muss mit der Steigung der Wendetangente übereinstimmen. Die Wendetangente hat überall die Steigung 3 also muss unsere Funktion auch die Steigung 3 an der Stelle haben.

f'(-2) = 3

f(-1) = 0

Du setzt in f(x) für x einfach -1 ein und setzt das ganze = 0

f(x) = ax³ + bx² + cx + d
f(-1) = a*(-1)^3 + b*(-1)^2 + c*(-1) + d = 0
f(-1) = -a + b - c + d = 0

So verfährst du mit allen Bedingungen. Du brauchst aber noch die 1. und 2. Ableitung

f(x) = ax³ + bx² + cx + d
f'(x) = 3ax^2 + 2bx + c
f''(x) = 6ax + 2b

---

Der_Mathcoach, sie haben ja gesagt das an der Stelle (2/-3,5) ein Wendepunkt existiert. Ist das ein echter Wendepunkt? Denn nach meiner Definition ist ein Wendpunkt ein Punkt in dem es kein Krümmungsverhalten gibt. Jedoch sehe ich in dem dazugehörigen Graph bei (2/-3,5) eine eindeutige rechts Krümmung, wie ist das möglich?

---

Meinst du den Punkt (2 | - 3.5) oder (- 2 | - 3.5) ???

Durch den ersten Punkt geht die Funktion denke ich überhaupt nicht. Beim Zweiten Punkt sehe ich einen Krümmungswechsel von einer Links in eine Rechtskrümmung.

Von daher kann ich dein Kommentar absolut nicht nachvollziehen.