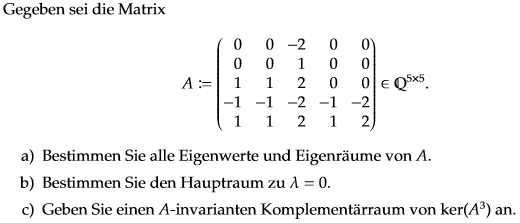
Erst mal meine bisherigen Ergebnisse:
Bei der a) habe ich als Eigenwerte λ1 = 0, λ2 = 0, λ3 = 1, λ4 = 1, λ5 = 1 und Eigenräume dann
Eig(0) = a * (-1 1 0 -2 1) <- das soll ein Vektor sein. und Eig(1) = a * (0 0 0 -1 1)
bei der b) habe ich Ker(A - 0*id)2 = {(-1 1 0 0 0), (0 0 0 -2 1)} <- das sollen übrigens wieder Vektoren sein.
ich hoffe mal das stimmt so weit und jetzt komm ich zu der Aufgabe wo ich nicht weiß was ich machen soll, der c). Wie gebe ich denn einen A-invarianten Komplementärraum an? Hoffe mir kann jemand helfen.