Beh: Lösungsmenge von <a,x-b>=0 mit xeR^n ist ein verschobener Unterraum b+H mit dimH=n-1.

Question

Seien a, b zwei Vektoren des R^n, wobei llall=1 bezüglich des Standard-Skalarprodukts gelte.

Wie zeigt man, dass die Lösungsmenge der Gleichung

<a,x-b>=0 mit xeR^n

ein verschobener Unterraum b+H mit dimH=n-1 ist ?

Answer 1

Nach der üblichen Definition von Skalarprodukt stehen wegen <a,x-b> = 0 die Vektoren x-b senkrecht auf a. Die folgende Skizze soll in 3-D zeigen, dass nun die Vektoren x von 0 aus auf Punkte auf der Ebene durch die Spitze von b liegen, die genau die Normalenebene zu a durch 0 ist (das H) aber verschoben um b.

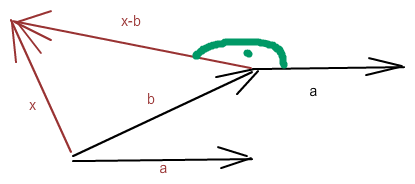
<a,x-b> = 0
<a,x> - <a,b> = 0

<a,x> = <a,b>, sieht dann im 3-dim. so aus wie die Koordinatenform einer Ebenengleichung
Ax + By + Cz = D

Eine Verallgemeinerung auf mehr Dimensionen muss nun vielleicht mit einem Induktionsbeweis gemacht werden (?).