Berechnen Sie, mit welcher Geschwindigkeit sich eine Gondel entlang der Kreisbahn bewegt.

Question

Ein Riesenrad mit 12 gleichmäßig verteilten Gondeln dreht sich mit konstanter Geschwindigkeit
gegen den Uhrzeigersinn.
Die Höhe h(t), in der sich eine Gondel zum Zeitpunkt t über
dem Boden befindet, ist:

h(t) = 15 ∙ sin( π/ 60 ∙ t + φ) + 20

t ... Zeit seit Beginn der Beobachtung in s
h(t) ... Höhe, in der sich eine Gondel zum Zeitpunkt t befindet, in m

– Berechnen Sie, mit welcher Geschwindigkeit (in km/h) sich eine Gondel entlang der Kreisbahn
bewegt.

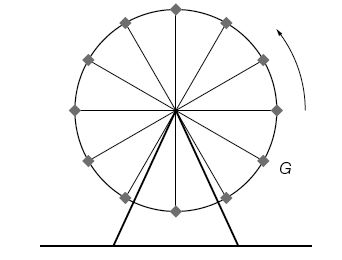
Die Gondel G befindet sich zur Zeit t = 0 s an der in der oben stehenden Skizze dargestellten
Position.

– Dokumentieren Sie in Worten, wie Sie den Parameter φ für die Funktion h der Gondel G ermitteln
können.

Answer 1

Berechnen Sie, mit welcher Geschwindigkeit (in km/h) sich eine Gondel entlang der Kreisbahn 
bewegt.

Mann kann die Periodendauer anhand von

pi/60 = 2pi/120

mit 120 Sekunden ablesen.

v = s / t = 2*pi*r / t = 2 * pi * 15 / 120 = 0.7854 m/s = 2.827 km/h

Dokumentieren Sie in Worten, wie Sie den Parameter φ für die Funktion h der Gondel G ermitteln können. 

Der Summand φ gibt eine Phasenverschiebung gegenober der normalen Sinusfunktion an. Die Gondel startet um 30 Grad versetzt zu der Normalen Sinusfunktion. Damit sollte φ den Wert -pi/6 haben.

Skizze:

~plot~15*sin(pi/60*x-pi/6)+20;[[0|120|0|50]]~plot~

Comments

wie weiß man bitte, dass die Funktion um 30° versetzt startet? Ich verstehe die Gegenüberstellung nicht ganz.