Bahnkurve mit Knick untersuchen.

Question

Hallo ich habe die Aufgabe folgende Bahnkurve zu untersuchen:

Skizzieren sie x(t) =(t^3,-t^2) mit t∈[-1,1] . Berechnen sie v ,a und erklären sie warum diese differenzierbare Kurve eine Spitze haben kann .Dieser spezielle Weg in der x-y Ebene kann als auch Graph einer Funktion aufgefasst werden , welche ist das?

v ist die erste Ableitung =(3t^2,-2t)

a ist die zweite Ableitung =(6t,-2)

Die spitze erkläre ich mir so , weil erstens für immer kleiner werdende x werte t^3 viel schneller gegen 0 strebt (wo die Funktion den Knick hat) als t^2 das heißt die y werte sind im vergleich zu x werten viel Betragsmäßig größer (da man ja im negativen quadranten liegt ) .

Und zweitens ist a =(6t,-2) bei der x Koordiante nicht Konstant sondern linear dh die Änderung der Steigung in x Richtung ist sinkend wobei sie in y richtung Konstant -2 ist .

Wie erklärt ihr die Spitze ?

Und welche funktion meint man hier?

Comments

Erklaeren sollst Du, weshalb es kein Widerspruch ist, dass der differenzierbare Weg x eine Spitze hat.

Answer 1

http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm

kennst Du ja schon -> Parameterdarstellung ergibt (wenn ich das Komma richtig interpretiere):

Wenn man beide Parameterfunktionen die 3. Wurzel zieht, kommt für die Wegfunktion heraus:

x(t)= -(t²)^{1/3} -> was das gleiche Bild als Liniendiagramm ergibt

Spitze ist nichts anderes als erst von -1 nach x=0 laufen -> und dann wieder zurück zu -1.

Allg. kann man auch den Lösungsweg umdrehen:

v(t) = ∫ a(t) dt

x(t) = ∫ v(t) dt

Gleichungssystem ->  Offset beachten -> fertig.

Comments

Hallo und danke !

Warum beschreibt nachdem man die 3te wurzel gezogen hat diese Funktion die bahnkurve ? Nimmt man dann einfach die y Koordinate,wenn die x Koordinate nurmehr t ist ? Bin da ein wenig verwirrt :D .

Ok die Spitze ist mir klar was das ist , warum kann sie auftreten ?

---

Dass man die 3. Wurzel für beide gleichzeitig ziehen darf, hatte ich ja schon beschrieben. Das ist nichts weiter, als die t-Schrittweite des Zeichnens (Abstand der Punkte) von nichtlinear auf linear zu ändern.

Man muss nur das Vorzeichen beachten.

Denkanstoß 1: -pow(x*x,1/3) = -pow(abs(x),2/3) =-[x²]^{1/3} = -|x|^{2/3}

Denkanstoß 2: Punkte=auto kann man die numerische Ableitung gestrichelt zeichnen lassen:

---

Hallo die Umformung kann och nachvollziehen , die Ableitungsfunktion ist unstetig für t =0 das kann man dann mit links und rechtsseitiger Grenzwert zeigen meinst du so ?

---

Ausgehend von meiner x(t) Funktion ergibt sich:

v(t)=d/dt -(t²)^{1/3} = -(2 t)/(3 (t^2)^{2/3}) = sgn(-t)*2/(3*abs(t)^{1/3})

a(t)=d/dt -(2 t)/(3 (t^2)^{2/3}) = sgn(-t)*2/(9 (t^2)^{2/3})

deshalb vermute ich, dass Deine Angaben

"v ist die erste Ableitung =(3t²,-2t) " falsch sind, das ergäbe diese Kurve für v:

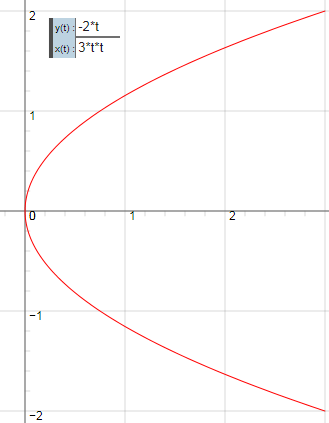
Das t in Deiner Aufgabe und in in meinem Diagramm bei Parameterdarstellung ist eine Laufvariable!!

Das t in der Physik ist die Zeit!! Nicht verwechseln!!

Die Ableitung v(t) = d x(t) / dt = x(t) ' {nach der Zeit ableiten}

Die Klammerschreibweise (t³,-t²) kann anders gemeint sein (deshalb oben der Hinweis, dass meine erste Interpretation Parameterdarstellung war!) -> andere Interpretation (abschnittsweise defenierte Liniendiagramm-Funktion):

x(t) = (t<0)?pow(t,3):-t*t

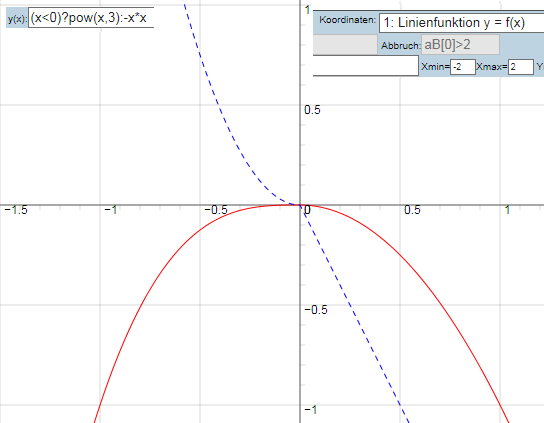
dann ist alles oben gesagte hinfällig!!!!

Mir kam es schon komisch vor, dass v und a Polstellen haben sollen, was physikalisch nicht geht!

---

Nach der anderen Komma- Interpretation gilt:

Die d/dt x(t) = v(t) = (x<0)?3*t²:-2*t siehe Bild, wobei deren Ableitung dann die abschnittsweise Beschleunigung a ist:

Das Wort "Spitze" gefällt mir nicht. Besser: Es gibt ein lokales Maximum (Hochpunkt) im gegebenen Intervall, da es eine Extremstelle ist mit x'(0) = 0 und

lim x->-0 x''(0) = 0

lim x->+0 x''(0) = -2 -> also nie positiv!

Bei dieser Interpretation wird fallend bis zum Punkt t=0 s beschleunigt (was einen Hochpunkt beim Weg x(t) ergibt), und ab t>0 konstant negativ beschleunigt, was "vom Hochpunkt wegbewegen" bedeutet.

---

Gemeint ist selbstredend eine Parameterdarstellung ("Bahnkurve") \(\pmb{x}(t)=(t^3,-t^2)\). Dein erstes Bild gehoert also zur Aufgabe. Zu erklaeren bleibt noch, wieso die Kurve eine "Spitze" hat, wo doch die Parameterdarstellung differenzierbar ist.

---

Ok und wie erklärt man sich die Spitze dann ?